题目内容
有下列四个命题:
①“若xy=1,则x、y互为倒数”的逆命题;
②“面积相等的三角形全等”的否命题;
③“若x2-2x+m=0有实根则m≤1”;
④“若A∩B=B,则A⊆B”的逆否命题.
其中真命题个数为( )
①“若xy=1,则x、y互为倒数”的逆命题;
②“面积相等的三角形全等”的否命题;
③“若x2-2x+m=0有实根则m≤1”;
④“若A∩B=B,则A⊆B”的逆否命题.
其中真命题个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①“若xy=1,则x、y互为倒数”的逆命题为:x、y互为倒数,则xy=1,利用倒数的定义即可判断出;
②“面积相等的三角形全等”的否命题为:面积不相等的三角形一定不全等,利用全等三角形的面积一定相等即可判断出;
③若x2-2x+m=0有实根则△=4-4m≥0,解得即可;
④“若A∩B=B,则A⊆B”不正确,利用其逆否命题与原命题等价即可得出.
②“面积相等的三角形全等”的否命题为:面积不相等的三角形一定不全等,利用全等三角形的面积一定相等即可判断出;
③若x2-2x+m=0有实根则△=4-4m≥0,解得即可;
④“若A∩B=B,则A⊆B”不正确,利用其逆否命题与原命题等价即可得出.
解答:
解:①“若xy=1,则x、y互为倒数”的逆命题为:x、y互为倒数,则xy=1,正确;
②“面积相等的三角形全等”的否命题为:面积不相等的三角形一定不全等,正确;
③若x2-2x+m=0有实根则△=4-4m≥0,解得m≤1,因此正确;
④若A∩B=B,则B⊆A,因此“若A∩B=B,则A⊆B”不正确,其逆否命题也不正确.
综上可得:只有C不正确.
故选:C.
②“面积相等的三角形全等”的否命题为:面积不相等的三角形一定不全等,正确;
③若x2-2x+m=0有实根则△=4-4m≥0,解得m≤1,因此正确;
④若A∩B=B,则B⊆A,因此“若A∩B=B,则A⊆B”不正确,其逆否命题也不正确.
综上可得:只有C不正确.
故选:C.
点评:本题考查了倒数的定义、全等三角形面积之间的关系、一元二次方程由实数根与判别式的关系、集合之间的关系等基础知识与基本技能方法,属于基础题.

练习册系列答案
相关题目
微积分基本定理:一般的,如果f(x)是区间[a,b]上的连续函数,并且F′(x)=f(x),那么∫
f(x)dx=( )
b a |
| A、F(a)-F(b) |
| B、F(b)-F(a) |
| C、F′(a)-F′(b) |
| D、F′(b)-F′(a) |
在△ABC中,若a<b<c,且c2<a2+b2,则△ABC为( )
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、不存在 |
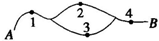 如图所示,在A、B间有四个焊接点1,2,3,4,若焊接点脱落导致断路,则电路,则电路不通,今发现A、B之间电路不通,则焊点脱落的不同情况有( )
如图所示,在A、B间有四个焊接点1,2,3,4,若焊接点脱落导致断路,则电路,则电路不通,今发现A、B之间电路不通,则焊点脱落的不同情况有( )| A、9种 | B、11种 |
| C、13种 | D、15种 |
某单位随机统计了某4天的用电量(度)与当天气温(℃)如下表,以了解二者的关系.
由表中数据得回归直线方程y=-2x+a,则a=( )
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
| A、60 | B、58 |
| C、40 | D、以上都不对 |
在0°~360°范围内,与-60°终边相同的角是( )
| A、30° | B、60° |
| C、300° | D、330° |
某班2013年元旦联欢会原定的9个歌唱节目已排成节目单,但在开演前又增加了两个新节目,如果将这两个节目插入原节目单中,那么不同插法的种数为( )
| A、110 | B、120 |
| C、20 | D、12 |