题目内容
已知a>0,函数f(x)=x-ax2-lnx.
(1)若f(x)是单调函数,求实数a的取值范围;
(2)若f(x)有两个极值点x1、x2,证明:f(x1)+f(x2)>3-2ln2.
(1)若f(x)是单调函数,求实数a的取值范围;
(2)若f(x)有两个极值点x1、x2,证明:f(x1)+f(x2)>3-2ln2.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)先求出函数的导数,通过讨论a的范围,满足函数f(x)是单调函数,从而求出a的范围,
(2)表示出f(x1)+f(x2)=lna+
+ln2+1,通过求导进行证明.
(2)表示出f(x1)+f(x2)=lna+
| 1 |
| 4a |
解答:
解:(1)∵f′(x)=-
,(x>0),
不妨设φ(x)=2ax2-x+1(x>0),
则关于x的方程2ax2-x+1=0的判别式△=1-8a,
当a≥
时,△≤0,φ(x)≥0,故f′(x)≤0,
∴函数f(x)在(0,+∞)上单调递减,
当0<a<
时,△>0,方程f′(x)=0有两个不相等的正根x1,x2,
不妨设x1<x2,则当x∈(0,x1)及x∈(x2,+∞)时f′(x)<0,
当x∈(x1,x2)时,f′(x)>0,f(x)不是单调函数,
综上,a的范围是[
,+∞),
(2)由(1)知当且仅当a∈(0,
)时f(x)有极小值x1 和极大值x2,
且x1,x2是方程的两个正根,则x1+x2=
,x1 x2=
,
∴f(x1)+f(x2)=(x1+x2)-a[(x1+x2)2-2x1 x2]-(lnx1+lnx2)
=ln(2a)+
+1=lna+
+ln2+1(0<a<
),
令g(a)=lna+
+ln2+1,
当a∈(0,
)时,g′(a)=
<0,
∴g(a)在(0,
)内单调递减,
故g(a)>g(
)=3-2ln2,
∴f(x1)+f(x2)>3-2ln2.
| 2ax2-x+1 |
| x |
不妨设φ(x)=2ax2-x+1(x>0),
则关于x的方程2ax2-x+1=0的判别式△=1-8a,
当a≥
| 1 |
| 8 |
∴函数f(x)在(0,+∞)上单调递减,
当0<a<
| 1 |
| 8 |
不妨设x1<x2,则当x∈(0,x1)及x∈(x2,+∞)时f′(x)<0,
当x∈(x1,x2)时,f′(x)>0,f(x)不是单调函数,
综上,a的范围是[
| 1 |
| 8 |
(2)由(1)知当且仅当a∈(0,
| 1 |
| 8 |
且x1,x2是方程的两个正根,则x1+x2=
| 1 |
| 2a |
| 1 |
| 2a |
∴f(x1)+f(x2)=(x1+x2)-a[(x1+x2)2-2x1 x2]-(lnx1+lnx2)
=ln(2a)+
| 1 |
| 4a |
| 1 |
| 4a |
| 1 |
| 8 |
令g(a)=lna+
| 1 |
| 4a |
当a∈(0,
| 1 |
| 8 |
| 4a-1 |
| 4a2 |
∴g(a)在(0,
| 1 |
| 8 |
故g(a)>g(
| 1 |
| 8 |
∴f(x1)+f(x2)>3-2ln2.
点评:本题考察了函数的单调性,导数的应用,不等式的证明,是一道综合题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
有下列四个命题:
①“若xy=1,则x、y互为倒数”的逆命题;
②“面积相等的三角形全等”的否命题;
③“若x2-2x+m=0有实根则m≤1”;
④“若A∩B=B,则A⊆B”的逆否命题.
其中真命题个数为( )
①“若xy=1,则x、y互为倒数”的逆命题;
②“面积相等的三角形全等”的否命题;
③“若x2-2x+m=0有实根则m≤1”;
④“若A∩B=B,则A⊆B”的逆否命题.
其中真命题个数为( )
| A、1 | B、2 | C、3 | D、4 |
| ∫ | 2 1 |
| 2 |
| x |
| A、e2-2ln2 |
| B、e2-e-2ln2 |
| C、e2+e+2ln2 |
| D、e2-e+2ln2 |
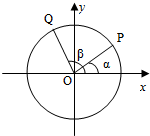 如图,以Ox为始边分别作角α与β(0<α<β<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(
如图,以Ox为始边分别作角α与β(0<α<β<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(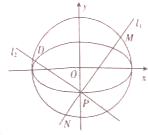 已知椭圆E:
已知椭圆E: 如图所示茎叶图记录了甲,乙两组各三名同学在期末考试中的数学成绩(满分为100分).乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.
如图所示茎叶图记录了甲,乙两组各三名同学在期末考试中的数学成绩(满分为100分).乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.