题目内容
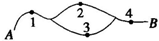如图所示，在A、B间有四个焊接点1，2，3，4，若焊接点脱落导致断路，则电路，则电路不通，今发现A、B之间电路不通，则焊点脱落的不同情况有（ ）| A、9种 | B、11种 |
| C、13种 | D、15种 |
考点：计数原理的应用
专题：排列组合
分析：由题意知本题是一个分步计数问题，每个焊接点都有脱落与不脱落两种状态，电路不通可能是1个或多个焊接点脱落，电路通的情况却只有3种，即2或3脱落或全不脱落，写出结果．
解答：
解：由题意知本题是一个分步计数问题，
每个焊接点都有脱落与不脱落两种状态，
电路不通可能是1个或多个焊接点脱落，问题比较复杂．
但电路通的情况却只有3种，
即2或3脱落或全不脱落．
∵每个焊接点有脱落与不脱落两种情况，
故共有24-3=13种情况．
故选：C．
每个焊接点都有脱落与不脱落两种状态，
电路不通可能是1个或多个焊接点脱落，问题比较复杂．
但电路通的情况却只有3种，
即2或3脱落或全不脱落．
∵每个焊接点有脱落与不脱落两种情况，
故共有24-3=13种情况．
故选：C．
点评：本题考查排列、组合及简单计数问题，是一个基础题，这种题目正面解起来比较困难，所以可以从反面来解决，这也是解排列组合问题的一种方法．
练习册系列答案
相关题目
设U=R，A={x|x≥1}，B={x|0＜x＜5}，则（∁UA）∩B=（ ）
| A、{x|0＜x＜1} |
| B、{x|1≤x＜5} |
| C、{x|0≤x＜1} |
| D、{x|1≤x＜5} |
有7个座位连成一排，安排3人就座，恰有3个空位相邻的不同坐法有（ ）
| A、36种 | B、48种 |
| C、72种 | D、96种 |
下列复数模大于3，且对应的点位于第三象限的为（ ）
| A、z=-2-i |
| B、z=2-3i |
| C、z=3+2i |
| D、z=-3-2i |
有下列四个命题：
①“若xy=1，则x、y互为倒数”的逆命题；
②“面积相等的三角形全等”的否命题；
③“若x2-2x+m=0有实根则m≤1”；
④“若A∩B=B，则A⊆B”的逆否命题．
其中真命题个数为（ ）
①“若xy=1，则x、y互为倒数”的逆命题；
②“面积相等的三角形全等”的否命题；
③“若x2-2x+m=0有实根则m≤1”；
④“若A∩B=B，则A⊆B”的逆否命题．
其中真命题个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
设函数f（x）=
x3+4x2-7x-2，则f′（1）=（ ）
| 1 |
| 3 |
| A、-2 | B、1 | C、0 | D、2 |
已知f（x），g（x）都是定义在R上的函数，且满足以下条件：
①f（x）为奇函数，g（x）为偶函数；
②f（1）=0，g（x）≠0；
③当x＞0时，总有f（x）•g′（x）＜f′（x）•g（x）．
则
＞0的解集为（ ）
①f（x）为奇函数，g（x）为偶函数；
②f（1）=0，g（x）≠0；
③当x＞0时，总有f（x）•g′（x）＜f′（x）•g（x）．
则
| f(x-2) |
| g(x-2) |
| A、（1，2）∪（3，+∞） |
| B、（-1，0）∪（1，+∞） |
| C、（-3，-2）∪（-1，+∞） |
| D、（-1，0）∪（3，+∞） |