题目内容
某单位随机统计了某4天的用电量(度)与当天气温(℃)如下表,以了解二者的关系.
由表中数据得回归直线方程y=-2x+a,则a=( )
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
| A、60 | B、58 |
| C、40 | D、以上都不对 |
考点:线性回归方程
专题:计算题,概率与统计
分析:根据所给的表格求出本组数据的样本中心点,结合样本中心点在线性回归直线上求得a值.
解答:
解:由题意,
=
(18+13+10-1)=10,
=
(24+34+38+64)=40
将(10,40)代入y=-2x+a,∴40=10×(-2)+a,
解得:a=60,
故选:A.
. |
| x |
| 1 |
| 4 |
. |
| y |
| 1 |
| 4 |
将(10,40)代入y=-2x+a,∴40=10×(-2)+a,
解得:a=60,
故选:A.
点评:本题考查回归直线方程,考查回归分析的初步应用.利用样本中心点在线性回归直线上是关键.

练习册系列答案
相关题目
下列符号判断错误的是( )
| A、sin156°>0 | ||
| B、cos(-96°)>0 | ||
C、tan
| ||
D、sin(-
|
设有一个回归方程为y=2-3x,变量x增加1个单位时,则y平均( )
| A、增加2个单位 |
| B、减少2个单位 |
| C、增加3个单位 |
| D、减少3个单位 |
有下列四个命题:
①“若xy=1,则x、y互为倒数”的逆命题;
②“面积相等的三角形全等”的否命题;
③“若x2-2x+m=0有实根则m≤1”;
④“若A∩B=B,则A⊆B”的逆否命题.
其中真命题个数为( )
①“若xy=1,则x、y互为倒数”的逆命题;
②“面积相等的三角形全等”的否命题;
③“若x2-2x+m=0有实根则m≤1”;
④“若A∩B=B,则A⊆B”的逆否命题.
其中真命题个数为( )
| A、1 | B、2 | C、3 | D、4 |
函数y=ln(3x-2)上过点(1,0)的切线方程( )
| A、y=x-1 |
| B、y=3x-3 |
| C、y=-x-1 |
| D、y=3x+1 |
已知点A(-3,1,4),则点A关于x轴的对称点的坐标为( )
| A、(-3,1,-4) |
| B、(3,-1,-4) |
| C、(-3,-1,-4) |
| D、(-3,1,-4) |
已知z=-
,则1+z50+z100的值为( )
| 1+i | ||
|
| A、i | B、1 | C、2+i | D、3 |
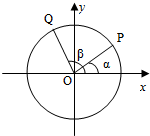 如图,以Ox为始边分别作角α与β(0<α<β<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(
如图,以Ox为始边分别作角α与β(0<α<β<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(