题目内容
某工厂有一容量为10吨的水池，水池中有进水管和出水管各一个，某天早晨同时打开进水管和出水管阀门，开始时池中蓄满了水，设经过x（小时）进水量P（吨）和出水量Q（吨）分别为P=2x，Q=8
．
（1）问经过多少小时，水池中的蓄水量y（吨）最小？并求出最小量．
（2）为防止水池中的水溢出，当水池再次蓄满水时，应关闭进水管阀门，问经过多少小时应关闭进水管阀门？
| x |
（1）问经过多少小时，水池中的蓄水量y（吨）最小？并求出最小量．
（2）为防止水池中的水溢出，当水池再次蓄满水时，应关闭进水管阀门，问经过多少小时应关闭进水管阀门？
考点：函数模型的选择与应用
专题：应用题,函数的性质及应用
分析：（1）根据经过x（小时）进水量P（吨）和出水量Q（吨）分别为P=2x，Q=8
，可得水池中的蓄水量y（吨），利用配方法可得结论；
（2）当y=10时关闭进水管阀门，此时2（
-2）2+2=10，求得x，即可得出结论．
| x |
（2）当y=10时关闭进水管阀门，此时2（
| x |
解答：
解：（1）y=2x-8
=2（
-2）2+2，当
=2时，y取最小值为2，此时x=4；
（2）当y=10时关闭进水管阀门，此时2（
-2）2+2=10，求得x=16．
| x |
| x |
| x |
（2）当y=10时关闭进水管阀门，此时2（
| x |
点评：本题考查函数模型的选择与应用，考查利用数学知识解决实际问题，比较基础．
练习册系列答案
相关题目
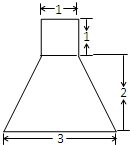
已知某空间几何体的正视图和侧视图相同，且如图所示，俯视图是两个同心圆，则它的表面积为（ ）
A、
| ||||
B、（12+4
| ||||
C、
| ||||
D、（13+4
|
已知sinα＞sinβ，α∈（-
，0），β∈（π，
π），则（ ）
| π |
| 2 |
| 3 |
| 2 |
| A、α+β＞π | ||
| B、α+β＜π | ||
C、α-β≥-
| ||
D、α-β≤-
|
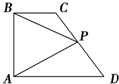如图，在直角梯形ABCD中，已知BC∥AD，AB⊥AD，AB=4，BC=2，AD=4，若P为CD的中点，则