题目内容
某地通过市场调查得到西红柿种植成本Q(单位:元/千克)与上市时间t(单位:50天)的数据如表:
(Ⅰ)根据表中数据,从下列函数中选取一个函数描述Q与t的变化关系,并求出函数的解析式;
Q=at+b,Q=at2+bt+c,Q=a•bt,Q=a•logbt
(Ⅱ)利用选取的函数,求西红柿最低种植成本及此时的上市天数.
| 时间t | 1 | 2 | 5 |
| 种植成本Q | 4 | 2 | 4 |
Q=at+b,Q=at2+bt+c,Q=a•bt,Q=a•logbt
(Ⅱ)利用选取的函数,求西红柿最低种植成本及此时的上市天数.
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(Ⅰ)由提供的数据知,描述西红柿种植成本Q与上市时间t的变化关系函数不可能是单调函数,故选取二次函数Q=at2+bt+c进行描述,将表格所提供的三组数据代入Q,即得函数解析式;
(Ⅱ)由二次函数的图象与性质可得,函数Q在t取何值时,有最小值.
(Ⅱ)由二次函数的图象与性质可得,函数Q在t取何值时,有最小值.
解答:
解:(Ⅰ)根据表中数据,表述西红柿种植成本Q与上市时间t的变化关系的函数不是单调函数,这与函数Q=at+b,Q=a•bt,Q=a•logbt均具有单调性不符,所以,在a≠0的前提下,可选取二次函数Q=at2+bt+c进行描述. …4分
把表格提供的三对数据代入该解析式得到
:…6分
解得a=
,b=-4,c=
. …9分
所以,西红柿种植成本Q与上市时间t的函数关系是Q=
t2-4t+
.…10分
(Ⅱ)Q=
t2-4t+
=Q=
(t-3)2+
当t=3,即在第150天时,西红柿种植成本Q最低为
(元/kg) …13分
把表格提供的三对数据代入该解析式得到
|
解得a=
| 2 |
| 3 |
| 22 |
| 3 |
所以,西红柿种植成本Q与上市时间t的函数关系是Q=
| 2 |
| 3 |
| 22 |
| 3 |
(Ⅱ)Q=
| 2 |
| 3 |
| 22 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
当t=3,即在第150天时,西红柿种植成本Q最低为
| 4 |
| 3 |
点评:本题考查了二次函数模型的应用,考查利用二次函数的图象与性质求函数的最值问题,确定函数模型是关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
设A(1,2),B(3,-1),C(3,4),则
•
( )
| AB |
| AC |
| A、11 | B、5 | C、-2 | D、1 |
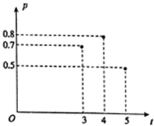 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足下列某函数关系:①p=at+b②p=alogbt③p=at2+bt+c(a,b,c是常数),如图记录了三次实验的数据,
加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足下列某函数关系:①p=at+b②p=alogbt③p=at2+bt+c(a,b,c是常数),如图记录了三次实验的数据,