题目内容
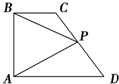 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则| PA |
| PB |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由题意和向量的线性运算求出
、
、
,再求出
和
,代入
•
利用向量的数量积运算化简即可.
| CD |
| DP |
| PC |
| PC |
| PB |
| PA |
| PB |
解答:
解:由题意可得,BC∥AD、BC=2,AD=4,则
=2
所以
=
+
+
=
+
,
因为P为CD的中点,所以
=
=-
=-
(
+
),
因为
=
+
=
-2
,
=
+
,且AB=4,BC=2,
则
•
=(
-2
)•(
+
)
=
(
-3
)•(-
)(
+3
)
=-
×(
2-9
2)=5,
故答案为:5.
| AD |
| BC |
所以
| CD |
| CB |
| BA |
| AD |
| BA |
| BC |
因为P为CD的中点,所以
| DP |
| PC |
| 1 |
| 2 |
| CD |
| 1 |
| 2 |
| BA |
| BC |
因为
| PA |
| PD |
| DA |
| PD |
| BC |
| PB |
| PC |
| CB |
则
| PA |
| PB |
| PD |
| BC |
| PC |
| CB |
=
| 1 |
| 2 |
| BA |
| BC |
| 1 |
| 2 |
| BA |
| BC |
=-
| 1 |
| 4 |
| BA |
| BC |
故答案为:5.
点评:本题考查向量的线性运算及其几何意义,以及向量数量积的运算,解题的关键是抓住向量的之间的关系,再结合已知条件化简.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
已知O为△ABC外一点,D为BC边上一点,且
+
-2
=0,若AB=3,AC=5.则
•
=( )
| OC |
| OB |
| OD |
| AD |
| BC |
| A、-8 | B、8 | C、-2 | D、2 |
设A(1,2),B(3,-1),C(3,4),则
•
( )
| AB |
| AC |
| A、11 | B、5 | C、-2 | D、1 |
已知函数f(x)=3-2|x|,g(x)=x2,构造函数F(x)=
,那么函数y=F(x)( )
|
| A、有最大值1,最小值-1 |
| B、有最小值-1,无最大值 |
| C、有最大值1,无最小值 |
| D、有最大值3,最小值1 |
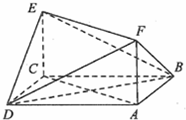 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=