题目内容
在四边形ABCD中，AB∥CD，AB=2CD，M，N分别为CD、BC的中点，若
=λ
+μ
，则λ+μ= ．
| AB |
| AM |
| AN |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：如图所示，连接MN并延长交AB的延长线于点E．由于AB∥CD，AB=2CD，M，N分别为CD、BC的中点，可得
=
=
=1，N是线段ME的中点，MC=EB=
AB．可得
=
+
，
=-
+
．与
=λ
+μ
比较即可得出．
| MN |
| NE |
| CN |
| NB |
| MC |
| EB |
| 1 |
| 4 |
| AN |
| 1 |
| 2 |
| AM |
| 1 |
| 2 |
| AE |
| AB |
| 4 |
| 5 |
| AM |
| 8 |
| 5 |
| AN |
| AB |
| AM |
| AN |
解答：
解：如图所示，连接MN并延长交AB的延长线于点E．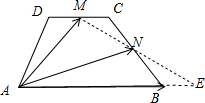
∵AB∥CD，AB=2CD，M，N分别为CD、BC的中点，
∴
=
=
=1，
∴N是线段ME的中点，MC=EB=
AB．
∴
=
+
=
+
，
化为
=-
+
．
∵
=λ
+μ
，
∴λ+μ=-
+
=
．
故答案为：
．
∵AB∥CD，AB=2CD，M，N分别为CD、BC的中点，
∴
| MN |
| NE |
| CN |
| NB |
| MC |
| EB |
∴N是线段ME的中点，MC=EB=
| 1 |
| 4 |
∴
| AN |
| 1 |
| 2 |
| AM |
| 1 |
| 2 |
| AE |
| 1 |
| 2 |
| AM |
| 5 |
| 8 |
| AB |
化为
| AB |
| 4 |
| 5 |
| AM |
| 8 |
| 5 |
| AN |
∵
| AB |
| AM |
| AN |
∴λ+μ=-
| 4 |
| 5 |
| 8 |
| 5 |
| 4 |
| 5 |
故答案为：
| 4 |
| 5 |
点评：本题考查了向量的平行四边形法则、向量共面定理，考查了辅助线的作法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
某校400名学生今年高考数学分数的频率分布直方图如图，则这400名学生中，分数在[90，110）之间的有