题目内容
已知等比数列{an}中，a1+a3是a2与a4的等差中项，且以a3-2，a3，a3+2为边长的三角形是直角三角形．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}满足b1=2，且bn+1=bn+an+n，求数列{bn}的通项公式．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}满足b1=2，且bn+1=bn+an+n，求数列{bn}的通项公式．
考点：等比数列的性质,数列递推式
专题：计算题,等差数列与等比数列
分析：（Ⅰ）利用以a3-2，a3，a3+2为边长的三角形是直角三角形，求出a3，利用a1+a3是a2与a4的等差中项，求出公比，即可求数列{an}的通项公式；
（Ⅱ）利用叠加法，可求数列{bn}的通项公式．
（Ⅱ）利用叠加法，可求数列{bn}的通项公式．
解答：
解：（Ⅰ）∵以a3-2，a3，a3+2为边长的三角形是直角三角形，
∴（a3-2）2+a32=（a3+2）2，
∵a3≠0，
∴a3=8，
∵a1+a3是a2与a4的等差中项，
∴2（a1+a3）=a2+a4，
∴2（
+8）=
+8q，
∴q=2，
∴an=2n；
（Ⅱ）∵bn+1=bn+an+n，
∴bn+1-bn=an+n，
∴bn-b1=（2+22+…+2n-1）+（1+2+…+n-1）=
+
，
∴bn=2n+
．
∴（a3-2）2+a32=（a3+2）2，
∵a3≠0，
∴a3=8，
∵a1+a3是a2与a4的等差中项，
∴2（a1+a3）=a2+a4，
∴2（
| 8 |
| q2 |
| 8 |
| q |
∴q=2，
∴an=2n；
（Ⅱ）∵bn+1=bn+an+n，
∴bn+1-bn=an+n，
∴bn-b1=（2+22+…+2n-1）+（1+2+…+n-1）=
| 2(1-2n-1) |
| 1-2 |
| n(n-1) |
| 2 |
∴bn=2n+
| n(n-1) |
| 2 |
点评：本题考查等比数列的通项，考查数列的求和，确定数列的通项是关键．
练习册系列答案
相关题目
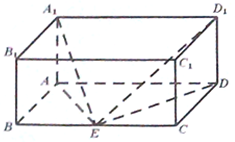如图，长方体ABCD-A1B1C1D1中，AB=AA1=1，AD=2，E是BC的中点
如图，已知ABC-A1B1C1是正三棱柱，它的底面边长和侧棱长都是2，D为侧棱CC1的中点，E为A1B1的中点．