题目内容
已知平面直角坐标系中，点P坐标为（3，4），将点P绕原点逆时针旋转
后，则点P的坐标为 ．
| π |
| 3 |
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：作出图形，求出OP，以及sin∠POx，cos∠POx，利用两角和与差的三角函数求出点P′的坐标，即可得解．
解答：
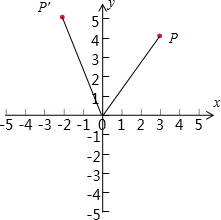解：如图，过点P作PA⊥x轴于点A，作PB⊥y轴于点B，过点P′作PA′⊥y轴于点A′，作PB′⊥x轴于点B′，
∵点P（3，4），
∴OPA=5，sin∠POx=
，cos∠POx=
∵点P（3，4）绕坐标原点逆时针旋转
得到点P′，
∴P′的横坐标为：5cos（∠POx+
）=5(
×
-
×
)=
，纵坐标为5sin（∠POx+
）=5(
×
+
×
)=
，
∴点P′的坐标是（
，
）．
故答案为：（
，
）．
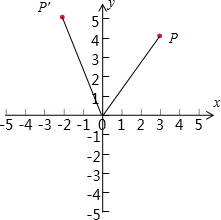解：如图，过点P作PA⊥x轴于点A，作PB⊥y轴于点B，过点P′作PA′⊥y轴于点A′，作PB′⊥x轴于点B′，∵点P（3，4），
∴OPA=5，sin∠POx=
| 4 |
| 5 |
| 3 |
| 5 |
∵点P（3，4）绕坐标原点逆时针旋转
| π |
| 3 |
∴P′的横坐标为：5cos（∠POx+
| π |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
3-4
| ||
| 2 |
| π |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| ||
| 2 |
4+3
| ||
| 2 |
∴点P′的坐标是（
3-4
| ||
| 2 |
4+3
| ||
| 2 |
故答案为：（
3-4
| ||
| 2 |
4+3
| ||
| 2 |
点评：本题考查了坐标与图形的变化-旋转，熟练掌握旋转变换的性质是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
已知平面上有A、B、C、D四点，这四点可确定的直线最多有（ ）
| A、4条 | B、6条 | C、8条 | D、10条 |