题目内容
满足25{x}+[x]=25的所有实数x的和是 (其中[x]表示不大于x的最大整数,{x}=x-[x]表示x的小数部分).
考点:函数的值
专题:函数的性质及应用
分析:由已知得25(x-[x])+[x]=25,x=1+0.96[x],[x]≤x<[x]+1,所以[x]≤1+0.96[x]<[x]+1,[x]=1,2,3,…,25,由此能求出满足25{x}+[x]=25的所有实数x的和.
解答:
解:25{x}+[x]=25,
25(x-[x])+[x]=25,
x=1+0.96[x],
而:[x]≤x<[x]+1
所以:[x]≤1+0.96[x]<[x]+1,
0≤1-0.04[x]<1,
-1≤-0.04[x]<0,
0<[x]≤25,
所以:[x]=1,2,3,…,25,
满足25{x}+[x]=25的所有实数x的和是:
(1+0.96×1)+(1+0.96×2)+(1+0.96×3)+…+(1+0.96×25)
=(1+1+1+…+1)+0.96×(1+2+3+…+25)
=25+0.96×(1+25)×
=337.
故答案为:337.
25(x-[x])+[x]=25,
x=1+0.96[x],
而:[x]≤x<[x]+1
所以:[x]≤1+0.96[x]<[x]+1,
0≤1-0.04[x]<1,
-1≤-0.04[x]<0,
0<[x]≤25,
所以:[x]=1,2,3,…,25,
满足25{x}+[x]=25的所有实数x的和是:
(1+0.96×1)+(1+0.96×2)+(1+0.96×3)+…+(1+0.96×25)
=(1+1+1+…+1)+0.96×(1+2+3+…+25)
=25+0.96×(1+25)×
| 25 |
| 2 |
=337.
故答案为:337.
点评:本题考查满足条件的实数和的求法,是中档题,解题时要认真审题.

练习册系列答案
相关题目
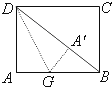 如图,矩形纸片ABCD,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,点A在BD上的落点为点A′,折痕为DG,则AG的长为
如图,矩形纸片ABCD,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,点A在BD上的落点为点A′,折痕为DG,则AG的长为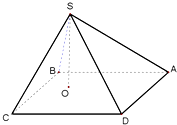 在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,顶点S在底面内的射影O在正方形ABCD的内部(不在边上),且SO=λa,λ为常数,设侧面SAB,SBC,SCD,SDA与底面ABCD所成的二面角依次为α1,α2,α3,α4,则下列各式为常数的是( )
在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,顶点S在底面内的射影O在正方形ABCD的内部(不在边上),且SO=λa,λ为常数,设侧面SAB,SBC,SCD,SDA与底面ABCD所成的二面角依次为α1,α2,α3,α4,则下列各式为常数的是( )