题目内容
已知动圆x2+y2-2mx-4my+6m-2=0恒过一个定点,这个定点的坐标是 .
考点:圆的一般方程
专题:直线与圆
分析:由已知得x2+y2-2=(2x+4y-6)m,从而
,由此能求出定点的坐标.
|
解答:
解:x2+y2-2mx-4my+6m-2=0,
∴x2+y2-2=(2x+4y-6)m,
∴
,
解得x=1,y=1,或x=
,y=
,
∴定点的坐标是(1,1),或(
,
).
故答案为:(1,1),或(
,
).
∴x2+y2-2=(2x+4y-6)m,
∴
|
解得x=1,y=1,或x=
| 1 |
| 5 |
| 7 |
| 5 |
∴定点的坐标是(1,1),或(
| 1 |
| 5 |
| 7 |
| 5 |
故答案为:(1,1),或(
| 1 |
| 5 |
| 7 |
| 5 |
点评:本题考查动圆经过的定点坐标的求法,是基础题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
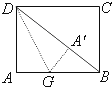 如图,矩形纸片ABCD,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,点A在BD上的落点为点A′,折痕为DG,则AG的长为
如图,矩形纸片ABCD,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,点A在BD上的落点为点A′,折痕为DG,则AG的长为