题目内容
若直线y=x+b与曲线x=
恰有一个公共点,则实数b的取值范围为 .
| 1-y2 |
考点:直线与圆的位置关系
专题:直线与圆
分析:曲线x=
表示以原点O(0,0)为圆心、半径等于1的半圆,数形结合求得当直线y=x+b与曲线x=
恰有一个公共点,则实数b的取值范围.
| 1-y2 |
| 1-y2 |
解答:
 解:曲线x=
解:曲线x=
即 x2+y2=1 (x≥0),表示以原点O(0,0)为圆心、半径等于1的半圆(位于y轴及y轴右侧的部分),
如图:当直线经过点A(0,-1)时,求得b=-1;
当直线经过点C(0,1)时,求得b=1;
当直线和圆相切时,由圆心到直线的距离等于半径可得
=1,求得b=
(舍去),或 b=-
,
数形结合可得当直线y=x+b与曲线x=
恰有一个公共点,则实数b的取值范围为(-1,1]∪{-
},
故答案为:(-1,1]∪{-
}.
 解:曲线x=
解:曲线x=| 1-y2 |
如图:当直线经过点A(0,-1)时,求得b=-1;
当直线经过点C(0,1)时,求得b=1;
当直线和圆相切时,由圆心到直线的距离等于半径可得
| |0-0+b| | ||
|
| 2 |
| 2 |
数形结合可得当直线y=x+b与曲线x=
| 1-y2 |
| 2 |
故答案为:(-1,1]∪{-
| 2 |
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
在△ABC中,三个内角A,B,C的对边分别为a,b,c,若a=2,b=2
,C=
,则内角A的值为( )
| 2 |
| π |
| 12 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
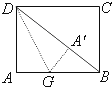 如图,矩形纸片ABCD,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,点A在BD上的落点为点A′,折痕为DG,则AG的长为
如图,矩形纸片ABCD,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,点A在BD上的落点为点A′,折痕为DG,则AG的长为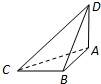 如图,已知球O的球面上四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=
如图,已知球O的球面上四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=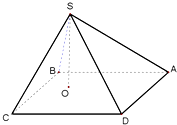 在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,顶点S在底面内的射影O在正方形ABCD的内部(不在边上),且SO=λa,λ为常数,设侧面SAB,SBC,SCD,SDA与底面ABCD所成的二面角依次为α1,α2,α3,α4,则下列各式为常数的是( )
在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,顶点S在底面内的射影O在正方形ABCD的内部(不在边上),且SO=λa,λ为常数,设侧面SAB,SBC,SCD,SDA与底面ABCD所成的二面角依次为α1,α2,α3,α4,则下列各式为常数的是( )