题目内容
已知函f(x)=2sin(x+
)cos(x+
)+2
cos2(x+
)-
为偶函数,且α∈[0,π].
(Ⅰ)求α的值;
(Ⅱ)若x为三角形ABC的一个内角,求满足f(x)=1的x的值.
| α |
| 2 |
| α |
| 2 |
| 3 |
| α |
| 2 |
| 3 |
(Ⅰ)求α的值;
(Ⅱ)若x为三角形ABC的一个内角,求满足f(x)=1的x的值.
考点:正弦函数的图象,函数奇偶性的性质
专题:三角函数的图像与性质
分析:(Ⅰ)利用辅助角公式将函数f(x)进行化简,即可求α的值;
(Ⅱ)若x为三角形ABC的一个内角,解方程f(x)=1,即可求的x的值.
(Ⅱ)若x为三角形ABC的一个内角,解方程f(x)=1,即可求的x的值.
解答:
解:(Ⅰ)f(x)=2sin(x+
)cos(x+
)+2
cos2(x+
)-
=sin(2x+α)+
cos(2x+α)=2sin(2x+α+
),
若f(x)为偶函数,则α+
=kπ+
,
即α=kπ+
,k∈Z,
∵α∈[0,π].
∴α=
;
(Ⅱ)∵α=
,
∴f(x)=2sin(2x+
+
)=2cos2x,
若x为三角形ABC的一个内角,由f(x)=1得
cos2x=
,
则2x=
或2x=
,
解得x=
或x=
.
| α |
| 2 |
| α |
| 2 |
| 3 |
| α |
| 2 |
| 3 |
| 3 |
| π |
| 3 |
若f(x)为偶函数,则α+
| π |
| 3 |
| π |
| 2 |
即α=kπ+
| π |
| 6 |
∵α∈[0,π].
∴α=
| π |
| 6 |
(Ⅱ)∵α=
| π |
| 6 |
∴f(x)=2sin(2x+
| π |
| 6 |
| π |
| 3 |
若x为三角形ABC的一个内角,由f(x)=1得
cos2x=
| 1 |
| 2 |
则2x=
| π |
| 3 |
| 5π |
| 3 |
解得x=
| π |
| 6 |
| 5π |
| 6 |
点评:本题主要考查三角函数的图象和性质,利用三角函数的奇偶性求出α是解决本题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
过抛物线y=x2上一点P(
,
)的切线的倾斜角是( )
| ||
| 2 |
| 3 |
| 4 |
| A、90° | B、45° |
| C、60° | D、30° |
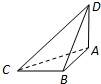 如图,已知球O的球面上四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=
如图,已知球O的球面上四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=