题目内容
已知向量
，
均为单位向量，他们的夹角为60°，实数x，y满足|x
+y
|=
，那么x+2y的最大值为 ．
| a |
| b |
| a |
| b |
| 3 |
考点：平面向量的综合题
专题：计算题,平面向量及应用
分析：先进行化简，把问题转化为一元二次方程有实数根即可求出．
解答：
解：∵向量
，
均为单位向量，它们的夹角为60°，
∴
•
=
∵实数x、y满足|x
+y
|=
，
∴两边平方化为y2+xy+x2-3=0．
设t=x+2y，则x=t-2y，
代入可得3y2-3ty+t2-3=0
把此方程看作关于y的一元二次方程且此方程有实数根，
则△=9t2-12（t2-3）≥0，解得t≤-2
或t≥2
．
∴x+2y的最大值为2
．
故答案为：2
．
| a |
| b |
∴
| a |
| b |
| 1 |
| 2 |
∵实数x、y满足|x
| a |
| b |
| 3 |
∴两边平方化为y2+xy+x2-3=0．
设t=x+2y，则x=t-2y，
代入可得3y2-3ty+t2-3=0
把此方程看作关于y的一元二次方程且此方程有实数根，
则△=9t2-12（t2-3）≥0，解得t≤-2
| 3 |
| 3 |
∴x+2y的最大值为2
| 3 |
故答案为：2
| 3 |
点评：熟练掌握数量积的运算和一元二次方程有实数根的充要条件是解题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
下列各组数据中，数值相等的是（ ）
| A、（25）10和（10110）2 |
| B、（13）10和（1101）2 |
| C、（11）10和（1100）2 |
| D、（10）10和（10）2 |
设有一个边长为3的正三角形，记为A1，将A1的每边三等份，在中间的线段上向图形外作正三角形，去掉中间的线段后所得到的图形记为A2；将A2的每边三等份，再重复上述过程，得到图形A3；再重复上述过程，得到图形A4，则A4的周长是（ ）
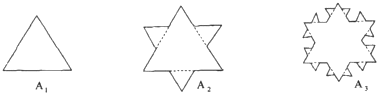
| A、12 | ||
| B、16 | ||
C、
| ||
D、
|
若将一个质点随机投入如图所示的正方形中，则质点落在由C1，C2所围成的图形内的概率为若函数f（x）=x3+ax2+3x-9在x=-1时取得极值，则a等于（ ）
| A、1 | B、2 | C、3 | D、4 |