题目内容
 若将一个质点随机投入如图所示的正方形中,则质点落在由C1,C2所围成的图形内的概率为
若将一个质点随机投入如图所示的正方形中,则质点落在由C1,C2所围成的图形内的概率为| ex-1 |
| e-1 |
| x |
考点:几何概型
专题:计算题,概率与统计
分析:利用几何槪型的概率公式,求出对应的图形的面积,利用面积比即可得到结论.
解答:
解:由题意,正方形的面积为1,由C1,C2所围成的图形的面积为
(
-
)dx=(
x
-
)
=
-
,
∴质点落在由C1,C2所围成的图形内的概率为
-
.
故答案为:
-
.
| ∫ | 1 0 |
| x |
| ex-1 |
| e-1 |
| 2 |
| 3 |
| 3 |
| 2 |
| ex-x |
| e-1 |
| | | 1 0 |
=
| 2 |
| 3 |
| e |
| e-1 |
∴质点落在由C1,C2所围成的图形内的概率为
| 2 |
| 3 |
| e |
| e-1 |
故答案为:
| 2 |
| 3 |
| e |
| e-1 |
点评:本题主要考查几何槪型的概率的计算,求出对应的图形的面积是解决本题的关键,比较基础.

练习册系列答案
相关题目
由于盐碱化严重,某地的耕地面积在最近50年内减少了10%.如果按此规律,设2012年的耕地面积为m,则2017年的耕地面积为( )
| A、(1-0.1250)m | ||
B、0.9
| ||
| C、0.9250m | ||
D、(1-0.9
|
已知平面向量
=(1,2),
=(-2,m),且
⊥
,则m=( )
| a |
| b |
| a |
| b |
| A、1 | B、4 | C、-4 | D、-1 |
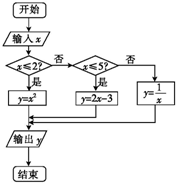 如图所示的程序框图,其作用是输入x的值,输出相应的y的值.
如图所示的程序框图,其作用是输入x的值,输出相应的y的值. 一个几何体的三视图如图,则这个几何体的体积为
一个几何体的三视图如图,则这个几何体的体积为