题目内容
 设椭圆E:
设椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
(Ⅰ)求椭圆E标准方程;
(Ⅱ)设P(x1,y1),Q(x2,y2)是椭圆E上的两点,
| m |
| 3 |
| n |
| 3 |
| m |
| n |
| OM |
| OP |
| OQ |
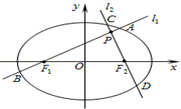
(Ⅲ)如图,若分别过椭圆E的左右焦点F1,F2的动直线?1,?2相交于P点,与椭圆分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率k1、k2、k3、k4满足k1+k2=k3+k4.是否存在定点M、N,使得|PM|+|PN|为定值.若存在,求出M、N点坐标;若不存在,说明理由.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(Ⅰ)首先,根据已知条件确定,a,b,c即可;
(Ⅱ)利用向量关系,建立关系式,然后,结合三角关系求解即可;
(Ⅲ)首先,对直线的斜率是否存在进行分类,然后,设直线的方程,联立方程组,建立关系式进行求解即可.
(Ⅱ)利用向量关系,建立关系式,然后,结合三角关系求解即可;
(Ⅲ)首先,对直线的斜率是否存在进行分类,然后,设直线的方程,联立方程组,建立关系式进行求解即可.
解答:
解:(Ⅰ)a=3,1-
=e2⇒
=1-
⇒b2=3,
所以椭圆标准方程
+
=1…(4分)
(Ⅱ)
•
=0⇒x1x2+3y1y2=0,
+3
=9,
+3
=9,M(x0,y0),
则(x0,y0)=(x1cosθ,y1cosθ)+(x2sinθ,y2sinθ)
=(x1cosθ+x2sinθ,y1cosθ+y2sinθ)(6分)
则
+3
=(x1cosθ+x2sinθ)2+3(y1cosθ+y2sinθ)2
=(
+3
)cos2θ+(
+3
)sin2θ+2sinθcosθ(x1x2+3y1y2)
=9(sin2θ+cos2θ)=9…(8分)
(Ⅲ)据题,得 F1(-
,0),F2(
,0),
当直线l1或l2斜率不存在时,
P点坐标为(-
,0)或(
,0),
当直线l1、l2斜率存在时,设斜率分别为m1,m2.
∴l1的方程为y=m1(x+
),l2的方程为y=m2(x-
).
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
联立方程组
,消去y,得,
(1+3
)x2+6
x+18
-9=0,
∴x1+x2=
,x1x2=
,
同理x3+x4=
,x3x4=
.…(9分)
∵k1=
=
=m1+
,k2=
=m1+
,k3=
=m2-
,k4=
=m2-
…(10分)
又满足k1+k2=k3+k4,
∴2m1+
=2m2-
⇒2m1+
=2m2-
⇒m1m2=-
设点P(x,y),则
•
=-
⇒
+
=1,(x≠±
)…(11分)
由当直线l1或l2斜率不存在时,P点坐标为(-
,0)或(
,0)也满足,
∴点P在椭圆
+
=1上,
则存在点M、N其坐标分别为(-
,0)、(
,0),使得|PM|+|PN|=2
为定值.…(12分)
| b2 |
| a2 |
| b2 |
| 9 |
| 6 |
| 9 |
所以椭圆标准方程
| x2 |
| 9 |
| y2 |
| 3 |
(Ⅱ)
| m |
| n |
| x | 2 1 |
| y | 2 1 |
| x | 2 2 |
| y | 2 2 |
则(x0,y0)=(x1cosθ,y1cosθ)+(x2sinθ,y2sinθ)
=(x1cosθ+x2sinθ,y1cosθ+y2sinθ)(6分)
则
| x | 2 0 |
| y | 2 0 |
=(
| x | 2 1 |
| y | 2 1 |
| x | 2 2 |
| y | 2 2 |
=9(sin2θ+cos2θ)=9…(8分)
(Ⅲ)据题,得 F1(-
| 6 |
| 6 |
当直线l1或l2斜率不存在时,
P点坐标为(-
| 6 |
| 6 |
当直线l1、l2斜率存在时,设斜率分别为m1,m2.
∴l1的方程为y=m1(x+
| 6 |
| 6 |
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
联立方程组
|
(1+3
| m | 2 1 |
| 6 |
| m | 2 1 |
| m | 2 1 |
∴x1+x2=
-6
| ||||
1+3
|
18
| ||
1+3
|
同理x3+x4=
6
| ||||
1+3
|
18
| ||
1+3
|
∵k1=
| y1 |
| x1 |
m1(x1+
| ||
| x1 |
| ||
| x1 |
| y2 |
| x2 |
| ||
| x2 |
| y3 |
| x3 |
| ||
| x3 |
| y4 |
| x4 |
| ||
| x4 |
又满足k1+k2=k3+k4,
∴2m1+
| ||
| x1x2 |
| ||
| x3x4 |
| ||||||
18
|
| ||||||
18
|
| 1 |
| 2 |
设点P(x,y),则
| y | ||
x+
|
| y | ||
x-
|
| 1 |
| 2 |
| x2 |
| 6 |
| y2 |
| 3 |
| 6 |
由当直线l1或l2斜率不存在时,P点坐标为(-
| 6 |
| 6 |
∴点P在椭圆
| x2 |
| 6 |
| y2 |
| 3 |
则存在点M、N其坐标分别为(-
| 3 |
| 3 |
| 6 |
点评:本题重点考查了椭圆的标准方程、椭圆的基本性质、直线与椭圆的位置关系等知识,属于难题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知f(x)=
,g(x)=2lnx,曲线y=f(x)在点(1,f(1))处的切线方程为2x-y-2=0.
(1)求a,b的值;
(2)若当x≥1时,g(x)≤mf(x)恒成立,求m的取值范围.
| ax2+b |
| x |
(1)求a,b的值;
(2)若当x≥1时,g(x)≤mf(x)恒成立,求m的取值范围.
已知某四棱台的三视图如图所示,则该四棱台的体积是( )


A、
| ||
| B、4 | ||
C、
| ||
| D、6 |
若f(x)是奇函数,且在(0,+∞)上是减函数,又有f(-2)=0,则不等式x•f(x)<0的解集为( )
| A、(-∞,-2)∪(2,+∞) |
| B、(-2,0)∪(0,2) |
| C、(-2,0)∪(2,+∞) |
| D、(-∞,-2)∪(0,2) |
设点M(-3,2
)是抛物线y2=2px(p>0)准线上一点,过该抛物线焦点F的直线与它交于A、B两点,若
•
=0,则△MAB的面积为( )
| 3 |
| FM |
| FA |
A、32
| ||
B、20
| ||
C、24
| ||
D、16
|