题目内容
已知某四棱台的三视图如图所示,则该四棱台的体积是( )


A、
| ||
| B、4 | ||
C、
| ||
| D、6 |
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:根据四棱台的三视图,得出该四棱台的结构特征是什么,由此计算它的体积即可.
解答:
解:根据四棱台的三视图,得:该四棱台是上、下底面为正方形,高为2的直四棱台,
且下底面正四边形的边长为2,上底面正四边形的边长为1;
∴该四棱台的体积为
V四棱台=
×(12+
+22)×2=
.
故选:C.
且下底面正四边形的边长为2,上底面正四边形的边长为1;
∴该四棱台的体积为
V四棱台=
| 1 |
| 3 |
| 12×22 |
| 14 |
| 3 |
故选:C.
点评:本题利用空间几何体的三视图求几何体的体积的应用问题,是基础题目.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
将4名新来的学生分到高三两个班,每班至少一人,不同的分配方法数为( )
| A、12 | B、16 | C、14 | D、18 |
若集合M={x|
<1},则∁RM等于( )
| 1 |
| x |
| A、{x|x≤1} |
| B、{x|0<x≤1} |
| C、{x|0≤x≤1} |
| D、{x|x<1} |
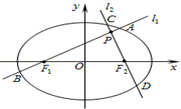 设椭圆E:
设椭圆E: