题目内容
袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是
.
(1)求n的值;
(2)(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.记事件A表示“a+b=2”,求事件A的概率.
| 2 |
| 3 |
(1)求n的值;
(2)(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.记事件A表示“a+b=2”,求事件A的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)由古典概型公式可得关于n的方程,解之即可;(2)由条件列举出所有可能的基本事件,找出符合的有几个,即可的答案.
解答:
解:(1)由题意可知:
=
,解得n=4.
(2)不放回地随机抽取2个小球的所有等可能基本事件为:
(0,1),(0,21),(0,22),(0,23),(0,24),
(1,0),(1,21),(1,22),(1,23),(1,24),
(21,0),(21,1),(21,22),(21,23),(21,24),
(22,0),(22,1),(22,21),(21,23),(21,24),
(23,0),(23,1),(23,21),(23,22),(23,24),
(24,0),(24,1),(24,21),(24,22),(24,23),
共30个,
事件A包含的基本事件为:(0,21),(0,22),(0,23),(0,24),(21,0),(22,0),(23,0),(24,0),共8个.
故事件A的概率P(A)=
=
| n |
| 1+1+n |
| 2 |
| 3 |
(2)不放回地随机抽取2个小球的所有等可能基本事件为:
(0,1),(0,21),(0,22),(0,23),(0,24),
(1,0),(1,21),(1,22),(1,23),(1,24),
(21,0),(21,1),(21,22),(21,23),(21,24),
(22,0),(22,1),(22,21),(21,23),(21,24),
(23,0),(23,1),(23,21),(23,22),(23,24),
(24,0),(24,1),(24,21),(24,22),(24,23),
共30个,
事件A包含的基本事件为:(0,21),(0,22),(0,23),(0,24),(21,0),(22,0),(23,0),(24,0),共8个.
故事件A的概率P(A)=
| 8 |
| 30 |
| 4 |
| 15 |
点评:本题为古典概型的求解,数准基本事件数是解决问题的关键,属基础题.

练习册系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程是y=
x,它的一个焦点在抛物线y2=48x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
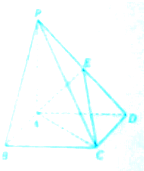 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,PA=AB,E为PO的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,PA=AB,E为PO的中点.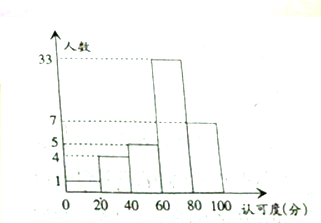 某校为了了解新的一轮教改模式有效性的“认可度”,在全校师生(可认为很多人)进行了“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”统计分析得如图
某校为了了解新的一轮教改模式有效性的“认可度”,在全校师生(可认为很多人)进行了“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”统计分析得如图