题目内容
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程是y=
x,它的一个焦点在抛物线y2=48x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出抛物线的准线方程,即有c=12,再由渐近线方程,可得a,b的关系,由a,b,c的关系式,得到a,b的方程,解得a,b,即可得到双曲线的方程.
解答:
解:抛物线y2=48x的准线为x=-12,
则双曲线的c=12,
由一条渐近线方程是y=
x,
则b=
a,
由c2=a2+b2=144,可得a=6,b=6
.
则双曲线的方程为
-
=1.
故选A.
则双曲线的c=12,
由一条渐近线方程是y=
| 3 |
则b=
| 3 |
由c2=a2+b2=144,可得a=6,b=6
| 3 |
则双曲线的方程为
| x2 |
| 36 |
| y2 |
| 108 |
故选A.
点评:本题考查抛物线和双曲线的方程、性质,考查渐近线方程和双曲线的a,b,c的关系,考查运算能力,属于基础题.

练习册系列答案
相关题目
某程序框图如图所示,则输出的结果S=( )
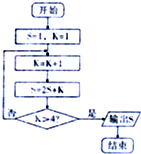

| A、11 | B、26 | C、57 | D、120 |
如图,一条直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50
,则抛物线的方程为( )
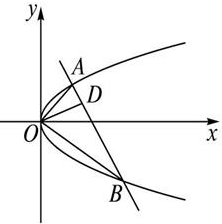
| 5 |

| A、y2=20x | ||
| B、y2=10x | ||
| C、y2=5x | ||
D、y2=
|
设i为虚数单位,则复数
=( )
| 3-4i |
| i |
| A、-4-3i | B、-4+3i |
| C、4+3i | D、4-3i |