题目内容

圆（x-3）2+（y-4）2=4上的点到直线x+y-14=0的最大距离
 
．
考点：直线与圆的位置关系
专题：计算题,直线与圆
分析：求出圆心和半径．再求出圆心到直线的距离，把此距离加上半径，即为所求．
解答： 解：（x-3）2+（y-4）2=4的圆心坐标为（3，4），半径为2，
（3，4）到直线的距离d=
|3+4-14|
2
=
7
2
2
，
∴圆（x-3）2+（y-4）2=4上的点到直线x+y-14=0的最大距离是
7
2
2
+2，
故答案为：
7
2
2
+2．
点评：本题考查直线和圆的位置关系，点到直线的距离公式等知识的综合应用，属于基础题．
练习册系列答案
相关题目
已知平行于直线2x-y+1=0的直线l与双曲线
x2
3
-
y2
2
=1交于A，B两点，且|AB|=4．
（1）求直线l的方程
（2）求△AOB的面积，O为原点．
袋子中放有大小和形状相同的小球若干个，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球n个．已知从袋子中随机抽取1个小球，取到标号是2的小球的概率是
2
3
．
（1）求n的值；
（2）（2）从袋子中不放回地随机抽取2个小球，记第一次取出的小球标号为a，第二次取出的小球标号为b．记事件A表示“a+b=2”，求事件A的概率．
已知|
a
|=4，|
b
|=2，且
a
与
b
的夹角为120°，求
（1）|
a
+
b
|；
（2）若（
a
+λ
b
）⊥（2
a
-3
b
），求λ的值．
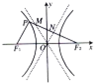已知点P是双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）左支上一点，F1、F2是双曲线的左、右两个焦点，且PF1⊥PF2，PF2与两条渐近线相交M，N两点（如图），点N恰好平分线段PF2，则双曲线的离心率是（　　）
A、
2
B、
3
C、2
D、
5
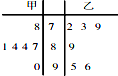甲乙两同学在高二年级的6次数学测验成绩（满分100分）如图茎叶图所示，则下列说法正确的是（　　）
A、甲乙同学的平均成绩相同，但是甲同学的成绩比乙稳定
B、甲乙同学的平均成绩相同，但是乙同学的成绩比甲稳定
C、甲同学的平均成绩比乙同学好，但是乙同学的成绩比甲稳定
D、乙同学的平均成绩比甲同学好，但是甲同学的成绩比乙稳定
已知函数f（x）=ex-e-x．
（1）判断函数f（x）的奇偶性；
（2）若函数f（x）在区间（a-1，a+1）上存在零点，求实数a的取值范围．
设i为虚数单位，则复数
3-4i
i
=（　　）
A、-4-3iB、-4+3i
C、4+3iD、4-3i
已知f（x）=sin（2x+
π
6
）．
（1）若将y=f（x）图象上的所有点向右平移
π
3
个单位长度，得到函数y=g（x）的图象，写出g（x）的表达式．
（2）求y=f（x）图象上所有对称点的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网