题目内容
已知函数f(x)=(x-x1)(x-x2)(x-x3),x1,x2,x3∈R,且x1<x2<x3.
(Ⅰ)当x1=0,x2=1,x3=2时,若方程f(x)=mx恰存在两个相等的实数根,求实数m的值;
(Ⅱ)求证:方程f′(x)=0有两个不相等的实数根;
(Ⅲ)若方程f'(x)=0的两个实数根是α,β(α<β),试比较
与α,β的大小并说明理由.
(Ⅰ)当x1=0,x2=1,x3=2时,若方程f(x)=mx恰存在两个相等的实数根,求实数m的值;
(Ⅱ)求证:方程f′(x)=0有两个不相等的实数根;
(Ⅲ)若方程f'(x)=0的两个实数根是α,β(α<β),试比较
| x1+x2 |
| 2 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:(Ⅰ)代值可把问题转化为x(x2-3x+2-m)=0,分类讨论可得;
(Ⅱ)求导数,证明方程的△>0即可;
(Ⅲ)由题意可得f′(
)=3(
-α)(
-β)<0,由不等式可得.
(Ⅱ)求导数,证明方程的△>0即可;
(Ⅲ)由题意可得f′(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
解答:
解:(Ⅰ)当x1=0,x2=1,x3=2时,
方程f(x)=mx可化为x(x-1)(x-2)=mx,即x(x2-3x+2-m)=0
方程f(x)=mx恰存在两个相等的实数根,包括两种情况:
①若x=0是方程x2-3x+2-m=0的根,则m=2时,方程x(x2-3x+2-m)=0可化为x2(x-3)=0,
则方程有两相等实根,一个为0,一个为3;
②若方程x2-3x+2-m=0有两相等的实根,则△=9-4(2-m)=0,解得m=-
,
此时方程x(x2-3x+2-m)=0有两个相等的实根,一个
,一个为0
∴当m=-
或m=2时,方程f(x)=mx恰存在两个相等的实数根;
(Ⅱ)由f(x)=(x-x1)(x-x2)(x-x3)可得f(x)=x3-(x1+x2+x3)x2+(x1x2+x1x3+x2x3)x-x1x2x3,
∴f′(x)=3x2-2(x1+x2+x3)x+(x1x2+x1x3+x2x3)=0,
∵△=4(x1+x2+x3)2-12(x1x2+x1x3+x2x3)=2[(x1-x2)2+(x2-x3)2+(x3-x1)2],
∵x1<x2<x3.∴△>0,∴方程f′(x)=0有两个不相等的实数根;
(Ⅲ)α<
<β,下面证明:
由f′(x)=3x2-2(x1+x2+x3)x+(x1x2+x1x3+x2x3)=0可得
f′(
)=
-(x1+x2+x3)(x1+x2)+x1x2+x1x3+x2x3-x1x2=-
<0
即f′(
)=3(
-α)(
-β)<0,
由α<β可得α<
<β,
方程f(x)=mx可化为x(x-1)(x-2)=mx,即x(x2-3x+2-m)=0
方程f(x)=mx恰存在两个相等的实数根,包括两种情况:
①若x=0是方程x2-3x+2-m=0的根,则m=2时,方程x(x2-3x+2-m)=0可化为x2(x-3)=0,
则方程有两相等实根,一个为0,一个为3;
②若方程x2-3x+2-m=0有两相等的实根,则△=9-4(2-m)=0,解得m=-
| 1 |
| 4 |
此时方程x(x2-3x+2-m)=0有两个相等的实根,一个
| 3 |
| 2 |
∴当m=-
| 1 |
| 4 |
(Ⅱ)由f(x)=(x-x1)(x-x2)(x-x3)可得f(x)=x3-(x1+x2+x3)x2+(x1x2+x1x3+x2x3)x-x1x2x3,
∴f′(x)=3x2-2(x1+x2+x3)x+(x1x2+x1x3+x2x3)=0,
∵△=4(x1+x2+x3)2-12(x1x2+x1x3+x2x3)=2[(x1-x2)2+(x2-x3)2+(x3-x1)2],
∵x1<x2<x3.∴△>0,∴方程f′(x)=0有两个不相等的实数根;
(Ⅲ)α<
| x1+x2 |
| 2 |
由f′(x)=3x2-2(x1+x2+x3)x+(x1x2+x1x3+x2x3)=0可得
f′(
| x1+x2 |
| 2 |
| 3(x1+x2)2 |
| 4 |
| (x1-x2)2 |
| 4 |
即f′(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
由α<β可得α<
| x1+x2 |
| 2 |
点评:本题考查根的存在性及个数的判断,涉及导数和一元二次方程根的关系,属中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
如图所示,程序框图(算法流程图)的输出结果是( )
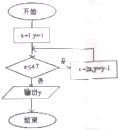

| A、0 | B、-1 | C、-2 | D、-3 |
下列命题错误的是( )
| A、已知直线a∥b,且b∥c,则a∥c |
| B、已知直线a∥平面α,且直线b∥平面α,则a∥b |
| C、已知直线a∥平面α,过平面α内一点作b∥a,则b?α |
| D、过平面外一点可以做无数条直线与这个平面平行,并且这些直线都在同一平面内 |
 如图,在△ABC中,D、E分别是AC、BC的中点,M是DE的中点,若
如图,在△ABC中,D、E分别是AC、BC的中点,M是DE的中点,若