题目内容
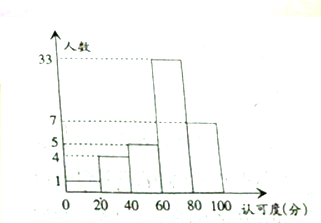 某校为了了解新的一轮教改模式有效性的“认可度”,在全校师生(可认为很多人)进行了“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”统计分析得如图
某校为了了解新的一轮教改模式有效性的“认可度”,在全校师生(可认为很多人)进行了“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”统计分析得如图(1)求这50名师生的“认可度”的平均值(每一区间取中点值计算)
(2)设表中个区间“认可度”分数的中点值构成集合A,那么从集合A中任取一值,记下该值后放回,然后再随机任选一个又记下该值后又放回,设第一次的值记为x,第二次的值记为y,求y>x的概率.
考点:列举法计算基本事件数及事件发生的概率,频率分布直方图
专题:概率与统计
分析:(1)根据频率分布表,和平均数的求法求出50名师生的“认可度”的平均值即可
(2)设表中个区间“认可度”分数的中点值构成集合A,则集合A={10,30,50,70,90},有放回的取两次,共有5×5=25种,其中满足其中y>x的有10种,根据概率公式计算即可
(2)设表中个区间“认可度”分数的中点值构成集合A,则集合A={10,30,50,70,90},有放回的取两次,共有5×5=25种,其中满足其中y>x的有10种,根据概率公式计算即可
解答:
解:(1)
=
(10×1+30×4+50×5+70×33+90×7)=66.4,
(2)设表中个区间“认可度”分数的中点值构成集合A,则集合A={10,30,50,70,90},
从集合A中任取一值,记下该值后放回,然后再随机任选一个又记下该值后又放回,共有5×5=25种,每一次为(x,y),包括如下:
(10,10),(10,30),(10,40),(10,70),(10,90),
(30,10),(30,30),(30,50),(30,70),(30,90),
(50,10),(50,30),(50,50),(50,70),(50,90),
(70,10),(70,30),(70,50),(70,70),(70,90),
(90,10),(90,30),(90,50),(90,70),(90,90),
其中y>x的(10,30),(10,40),(10,70),(10,90),(30,50),(30,70),(30,90),(50,70),(50,90),(70,90)共10种,
故y>x的概率P=
=
. |
| x |
| 1 |
| 50 |
(2)设表中个区间“认可度”分数的中点值构成集合A,则集合A={10,30,50,70,90},
从集合A中任取一值,记下该值后放回,然后再随机任选一个又记下该值后又放回,共有5×5=25种,每一次为(x,y),包括如下:
(10,10),(10,30),(10,40),(10,70),(10,90),
(30,10),(30,30),(30,50),(30,70),(30,90),
(50,10),(50,30),(50,50),(50,70),(50,90),
(70,10),(70,30),(70,50),(70,70),(70,90),
(90,10),(90,30),(90,50),(90,70),(90,90),
其中y>x的(10,30),(10,40),(10,70),(10,90),(30,50),(30,70),(30,90),(50,70),(50,90),(70,90)共10种,
故y>x的概率P=
| 10 |
| 25 |
| 2 |
| 5 |
点评:本题考查了等可能事件的概率,关键是一一列举出所有的基本事件,属于基础题

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
某程序框图如图所示,则输出的结果S=( )
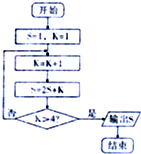

| A、11 | B、26 | C、57 | D、120 |
已知
=(2,4,x),
=(2,y,2),若|
|=6,
⊥
,则x+y的值是( )
| a |
| b |
| a |
| a |
| b |
| A、-3或1 | B、3或-1 |
| C、-3 | D、1 |
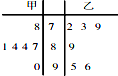 甲乙两同学在高二年级的6次数学测验成绩(满分100分)如图茎叶图所示,则下列说法正确的是( )
甲乙两同学在高二年级的6次数学测验成绩(满分100分)如图茎叶图所示,则下列说法正确的是( )| A、甲乙同学的平均成绩相同,但是甲同学的成绩比乙稳定 |
| B、甲乙同学的平均成绩相同,但是乙同学的成绩比甲稳定 |
| C、甲同学的平均成绩比乙同学好,但是乙同学的成绩比甲稳定 |
| D、乙同学的平均成绩比甲同学好,但是甲同学的成绩比乙稳定 |