题目内容
如果二次方程x2-px-q=0（p，q∈N*） 的正根小于3，那么这样的二次方程有（ ）
| A、5个 | B、6个 | C、7个 | D、8个 |
考点：一元二次方程的根的分布与系数的关系
专题：函数的性质及应用
分析：利用判别式先判断根的取值情况，利用正根小于3，得到条件关系即可求解．
解答：
解：由△=p2+4q＞0，可知方程有两个不同是实根，又两根之积为-q＜0，
所以方程的根为一正一负．
设f（x）=x2-px-q，则满足f（3）＞0，即f（3）=9-3p-q＞0，
即 3p+q＜9．
由于p，q∈N*，所以 p=1时，q≤5 或p=2，q≤2．于是共有7组（p，q）符合题意．
故选 C．
所以方程的根为一正一负．
设f（x）=x2-px-q，则满足f（3）＞0，即f（3）=9-3p-q＞0，
即 3p+q＜9．
由于p，q∈N*，所以 p=1时，q≤5 或p=2，q≤2．于是共有7组（p，q）符合题意．
故选 C．
点评：本题主要考查一元二次方程根的分布，利用一元二次方程和函数之间的关系，将方程转化为函数关系来求解，考查学生的转化能力．
练习册系列答案
相关题目
在正方体ABCD-
中，M是棱AB的中点，则异面直线DM与
B所成角的余弦值为（ ）
| A | 1 |
| B | 1 |
| C | 1 |
| D | 1 |
| D | 1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
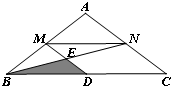如图所示，在△ABC中，AB=AC=10cm，BC=16cm，M、N、D分别是AB、AC、BC的中点，连接DM、BN交于点E，则图中阴影部分△BDE的面积为（ ）| A、4cm2 |
| B、6cm2 |
| C、8cm2 |
| D、12cm2 |