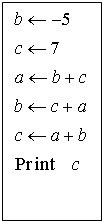题目内容
对于正整数n,若n=pq(p≥q,且p,q为整数),当p-q最小时,则称pq为n的“最佳分解”,并规定f(n)=
(如12的分解有12×1,6×2,4×3,其中,4×3为12的最佳分解,则f(n)=
.关于f(n)有下列判断:
①f(9)=0;
②f(11)=
;
③f(24)=
;
④f(2013)=
.
其中,正确判断的序号是 .
| q |
| p |
| 3 |
| 4 |
①f(9)=0;
②f(11)=
| 1 |
| 11 |
③f(24)=
| 3 |
| 8 |
④f(2013)=
| 33 |
| 61 |
其中,正确判断的序号是
考点:函数的值
专题:计算题,新定义
分析:将各个数的分解因式写出,利用f(n)的定义求出求出各个f(n),从而判断出各命题的正误.
解答:
解:对于①,因为9=1×9; 3×3;9×1 所以f(9)=1,故①不正确;
对于②,因为11=11×1; 11=1×11;所以f(11)=
,故②正确;
对于③,对于②,因为24=1×24; 24=2×12; 24=3×8; 24=4×6所以f(24)=
,故③不正确;
对于④,因为2013=2013×1,2013=61×33,2013=33×61,2013=1×2013,所以f(2013)=
,故④正确.
故答案为:②④.
对于②,因为11=11×1; 11=1×11;所以f(11)=
| 1 |
| 11 |
对于③,对于②,因为24=1×24; 24=2×12; 24=3×8; 24=4×6所以f(24)=
| 4 |
| 6 |
对于④,因为2013=2013×1,2013=61×33,2013=33×61,2013=1×2013,所以f(2013)=
| 33 |
| 61 |
故答案为:②④.
点评:本题考查通过题中的新定义解题,关键理解新定义.新定义题是常考的题型要重视.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
已知等比数列{an},Sn为其前n项和,S3=10,S6=30,则S9=( )
| A、50 | B、60 | C、70 | D、90 |
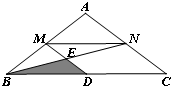 如图所示,在△ABC中,AB=AC=10cm,BC=16cm,M、N、D分别是AB、AC、BC的中点,连接DM、BN交于点E,则图中阴影部分△BDE的面积为( )
如图所示,在△ABC中,AB=AC=10cm,BC=16cm,M、N、D分别是AB、AC、BC的中点,连接DM、BN交于点E,则图中阴影部分△BDE的面积为( )| A、4cm2 |
| B、6cm2 |
| C、8cm2 |
| D、12cm2 |