题目内容
18.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0)的一条渐近线为y=$\sqrt{3}$x,则离心率e等于( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 由题意得$\frac{b}{a}$=$\sqrt{3}$,利用e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=2,可得结论.
解答 解:由题意得$\frac{b}{a}$=$\sqrt{3}$,
∴e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=2.
故选:D.
点评 本题考查双曲线的离心率的性质和应用,解题时要注意公式的合理运用.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
9.若等比数列{an}满足a2•a4=$\frac{1}{2}$,则a1a32a5=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
13.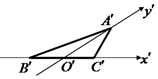 如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=$\sqrt{6}$,A′O′=$\frac{\sqrt{3}}{4}$,那么△ABC的面积是( )
如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=$\sqrt{6}$,A′O′=$\frac{\sqrt{3}}{4}$,那么△ABC的面积是( )
 如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=$\sqrt{6}$,A′O′=$\frac{\sqrt{3}}{4}$,那么△ABC的面积是( )
如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=$\sqrt{6}$,A′O′=$\frac{\sqrt{3}}{4}$,那么△ABC的面积是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 3$\sqrt{2}$ |
3.已知等差数列{an}中,a1+a5=20,a9=20,则a6=( )
| A. | 15 | B. | 20 | C. | 25 | D. | 30 |
10.在锐角△ABC中,sinA=$\frac{2\sqrt{6}}{5}$,cosC=$\frac{5}{7}$,BC=7,若动点P满足$\overrightarrow{AP}$=$\frac{λ}{2}$$\overrightarrow{AB}$+(1-λ)$\overrightarrow{AC}$(λ∈R),则点P轨迹与直线AB,AC所围成的封闭区域的面积( )
| A. | 3$\sqrt{6}$ | B. | 4$\sqrt{6}$ | C. | 6$\sqrt{6}$ | D. | 12$\sqrt{6}$ |
8.$\sqrt{1-2sin(\frac{π}{2}+2)cos(\frac{π}{2}+2)}$的值是( )
| A. | sin2-cos2 | B. | cos2-sin2 | C. | -(sin2+cos2) | D. | sin2+cos2 |
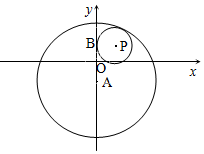 已知圆A:x2+(y+3)2=100,圆A内一定点B(0,3),圆P过B且与圆A内切,如图所示,求圆心P的轨迹方程.
已知圆A:x2+(y+3)2=100,圆A内一定点B(0,3),圆P过B且与圆A内切,如图所示,求圆心P的轨迹方程.