题目内容
7．
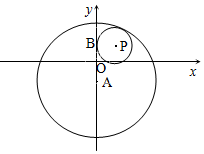已知圆A：x2+（y+3）2=100，圆A内一定点B（0，3），圆P过B且与圆A内切，如图所示，求圆心P的轨迹方程．
分析 设动圆圆心P，半径为r，利用两圆相切内切，两圆心距和两半径之间的关系列出PA和PB的关系式，正好符合椭圆的定义，利用定义法求轨迹方程即可．
解答 解：∵|PA|+|PB|=10-r+r=10＞6=|AB|
∴P的轨迹是以A、B两点为焦点的椭圆，2a=10得a=5，c=3，∴b=4
所以圆心P的轨迹方程为$\frac{x^2}{16}+\frac{y^2}{25}=1$．
点评 本题考查两圆的位置关系的应用和定义法求轨迹方程，综合性较强．
练习册系列答案
名校课堂系列答案
相关题目
18．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0）的一条渐近线为y=$\sqrt{3}$x，则离心率e等于（ ）
| A． | $\sqrt{2}$ | B． | $\frac{3}{2}$ | C． | $\sqrt{3}$ | D． | 2 |
12．已知i为虚数单位，复数z满足$\frac{z}{z-i}$=i，则z=（ ）
| A． | $\frac{1}{2}+\frac{1}{2}i$ | B． | $\frac{1}{2}-\frac{1}{2}i$ | C． | $-\frac{1}{2}+\frac{1}{2}i$ | D． | $-\frac{1}{2}-\frac{1}{2}i$ |
17．已知等差数列{an}的首项为$\frac{1}{2}$，Sn为数列的前n项和，若S6=2S4，则a10=（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{19}{2}$ | C． | $\frac{5}{2}$ | D． | $\frac{7}{2}$ |