题目内容
13．
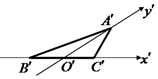如图是水平放置的△ABC按“斜二测画法”得到的直观图，其中B′O′=C′O′=$\sqrt{6}$，A′O′=$\frac{\sqrt{3}}{4}$，那么△ABC的面积是（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\frac{3\sqrt{2}}{2}$ | D． | 3$\sqrt{2}$ |
分析 ′O′=C′O′=$\sqrt{6}$，A′O′=$\frac{\sqrt{3}}{4}$，直接计算△ABC即可．
解答 解：因为B′O′=C′O′=$\sqrt{6}$，A′O′=$\frac{\sqrt{3}}{4}$，
所以△ABC的面积为$\frac{1}{2}×2\sqrt{6}×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{2}}{2}$．
故选C．
点评 本题考查斜二测画法中原图和直观图面积之间的关系，属基本运算的考查．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
3．命题：若x+y≠5则x≠2或y≠3（ ）
| A． | 真命题 | B． | 假命题 | C． | 无法判断真假 | D． | 不确定 |
8．已知点O是锐角△ABC的外心，a，b，c分别为内角A、B、C的对边，A=$\frac{π}{4}$，且$\frac{cosB}{sinC}$$\overrightarrow{AB}$+$\frac{cosC}{sinB}$$\overrightarrow{AC}$=λ$\overrightarrow{OA}$，则λ的值为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | -$\frac{{\sqrt{2}}}{2}$ | C． | $\sqrt{2}$ | D． | -$\sqrt{2}$ |
18．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0）的一条渐近线为y=$\sqrt{3}$x，则离心率e等于（ ）
| A． | $\sqrt{2}$ | B． | $\frac{3}{2}$ | C． | $\sqrt{3}$ | D． | 2 |
5．等比数列{an}的前n项和Sn=$\frac{1}{2}$3n+1-a，则a等于（ ）
| A． | $\frac{3}{2}$ | B． | $-\frac{3}{2}$ | C． | $\frac{1}{2}$ | D． | $-\frac{1}{2}$ |
3．
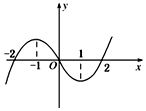在R上可导的函数f（x）的图象如图示，f′（x）为函数f（x）的导数，则关于x的不等式x•f′（x）＜0的解集为（ ）
在R上可导的函数f（x）的图象如图示，f′（x）为函数f（x）的导数，则关于x的不等式x•f′（x）＜0的解集为（ ）| A． | （-∞，-1）∪（0，1） | B． | （-2，-1）∪（1，2） | C． | （-1，0）∪（1，+∞） | D． | （-∞，-2）∪（2，+∞） |