题目内容
函数y=
的连续区间为 .
| ||
| x3-1 |
考点:函数的连续性
专题:函数的性质及应用
分析:对于函数y=
,只要分母不为零,函数就连续,求得x的范围,可得函数的连续区间.
| ||
| x3-1 |
解答:
解:对于函数y=
,只要分母不为零,函数就连续,由x3-1≠0,
求得x≠1,故函数的连续区间为(-∞,1)、(1,+∞),
故答案为:(-∞,1)、(1,+∞).
| ||
| x3-1 |
求得x≠1,故函数的连续区间为(-∞,1)、(1,+∞),
故答案为:(-∞,1)、(1,+∞).
点评:本题主要考查函数的连续性,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知线段PQ=
如图,已知线段PQ=| 2 |
| π |
| 2 |
A、 |
B、 |
C、 |
D、 |
设两直线l1:x+y
+b=0,l2:xsinθ+y
-a=0,θ∈(π,
π),则直线l1和l2的位置关系是( )
| 1-cosθ |
| 1+cosθ |
| 3 |
| 2 |
| A、平行 | B、平行或重合 |
| C、垂直 | D、相交但不一定垂直 |

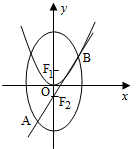 如图所示,椭圆C:
如图所示,椭圆C: