题目内容
在数列{an}中,已知a1=1,且an+1=
.
(1)求a2,a3,a4;
(2)猜想数列{an}的通项公式;
(3)试用数学归纳法证明(2)中猜想.
| an |
| 2+an |
(1)求a2,a3,a4;
(2)猜想数列{an}的通项公式;
(3)试用数学归纳法证明(2)中猜想.
考点:数学归纳法,数列递推式
专题:计算题,证明题,等差数列与等比数列,点列、递归数列与数学归纳法
分析:(1)利用数列递推式,代入计算可得结论;
(2)由a1=
,a2=
,a3=
,a4=
,即可猜想得到通项公式;
(3)利用(2)的猜想an的表达式,运用数学归纳法证明.注意两个步骤缺一不可,特别必须运用假设证明n=k+1,也成立.
(2)由a1=
| 1 |
| 2-1 |
| 1 |
| 22-1 |
| 1 |
| 23-1 |
| 1 |
| 24-1 |
(3)利用(2)的猜想an的表达式,运用数学归纳法证明.注意两个步骤缺一不可,特别必须运用假设证明n=k+1,也成立.
解答:
解:(1)∵a1=1,an+1=
,
∴a2=
=
,a3=
=
,a4=
=
.
(2)由(1),a1=
,a2=
,a3=
,a4=
,
可以猜想an=
.
(3)用数学归纳法证明:
ⅰ)当n=1时,a1=
=1,所以当n=1时猜想成立.
ⅱ)假设当n=k(k∈N*)时猜想成立,即ak=
,
当n=k+1时,ak+1=
=
=
,
所以当n=k+1时猜想也成立.
由ⅰ)和ⅱ)可知,猜想对任意的n∈N*都成立.
所以an=
.
| an |
| an+2 |
∴a2=
| a1 |
| 2+a1 |
| 1 |
| 3 |
| a2 |
| 2+a2 |
| 1 |
| 7 |
| a3 |
| 2+a3 |
| 1 |
| 15 |
(2)由(1),a1=
| 1 |
| 2-1 |
| 1 |
| 22-1 |
| 1 |
| 23-1 |
| 1 |
| 24-1 |
可以猜想an=
| 1 |
| 2n-1 |
(3)用数学归纳法证明:
ⅰ)当n=1时,a1=
| 1 |
| 1 |
ⅱ)假设当n=k(k∈N*)时猜想成立,即ak=
| 1 |
| 2k-1 |
当n=k+1时,ak+1=
| ak |
| 2+ak |
| ||
2+
|
| 1 |
| 2k+1-1 |
所以当n=k+1时猜想也成立.
由ⅰ)和ⅱ)可知,猜想对任意的n∈N*都成立.
所以an=
| 1 |
| 2n-1 |
点评:本题考查数列递推式,考查数列的通项,考查数学归纳法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
设两直线l1:x+y
+b=0,l2:xsinθ+y
-a=0,θ∈(π,
π),则直线l1和l2的位置关系是( )
| 1-cosθ |
| 1+cosθ |
| 3 |
| 2 |
| A、平行 | B、平行或重合 |
| C、垂直 | D、相交但不一定垂直 |
若{x}表示“不小于x的最小整数”(如{1,2}=2),则当-3≤x≤3时,方程{x-1}=x的实数解有( )
| A、0个 | B、5个 | C、6个 | D、7个 |
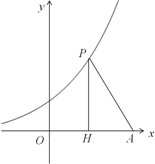 如图,已知点A(10,0),直线x=t(0<t<10)与函数y=e2x+1的图象交于点P,与x轴交于点H,记△APH的面积为f(t).
如图,已知点A(10,0),直线x=t(0<t<10)与函数y=e2x+1的图象交于点P,与x轴交于点H,记△APH的面积为f(t).