题目内容
已知f(x)是定义域在R上的奇函数,若x>0时,f(x)=x3-
,则f(x)在R上的解析式是 .
| 1 |
| x-3 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:f(x)在R上是奇函数,所以f(0)=0,要求f(x)在R上的解析式还需求x<0时f(x)解析式:设x<0,-x>0,所以f(-x)=-x3-
=-f(x),所以这即可求出x<0的解析式,所以最后分段写出f(x)在R上的解析式即可.
| 1 |
| -x-3 |
解答:
解:设x<0,-x>0,则:
f(-x)=(-x)3-
=-x3+
=-f(x);
∴f(x)=x3-
;
又f(0)=0;
∴f(x)在R上的解析式为:f(x)=
.
故答案为:f(x)=
.
f(-x)=(-x)3-
| 1 |
| -x-3 |
| 1 |
| x+3 |
∴f(x)=x3-
| 1 |
| x+3 |
又f(0)=0;
∴f(x)在R上的解析式为:f(x)=
|
故答案为:f(x)=
|
点评:考查奇函数的定义,已知x>0的f(x)的解析式求x<0的f(x)解析式的方法,奇函数定义域包括x=0时,f(0)=0,以及分段函数的概念及表示.

练习册系列答案
相关题目
设两直线l1:x+y
+b=0,l2:xsinθ+y
-a=0,θ∈(π,
π),则直线l1和l2的位置关系是( )
| 1-cosθ |
| 1+cosθ |
| 3 |
| 2 |
| A、平行 | B、平行或重合 |
| C、垂直 | D、相交但不一定垂直 |
已知集合M={m|(m-11)(m-16)≤0,m∈N},若(x3-
)n(n∈M)的二项展开式中存在常数项,则n等于( )
| 1 |
| x2 |
| A、16 | B、15 | C、14 | D、12 |
若{x}表示“不小于x的最小整数”(如{1,2}=2),则当-3≤x≤3时,方程{x-1}=x的实数解有( )
| A、0个 | B、5个 | C、6个 | D、7个 |
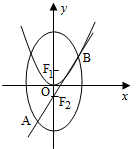 如图所示,椭圆C:
如图所示,椭圆C: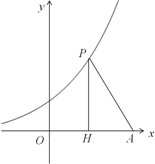 如图,已知点A(10,0),直线x=t(0<t<10)与函数y=e2x+1的图象交于点P,与x轴交于点H,记△APH的面积为f(t).
如图,已知点A(10,0),直线x=t(0<t<10)与函数y=e2x+1的图象交于点P,与x轴交于点H,记△APH的面积为f(t).