题目内容
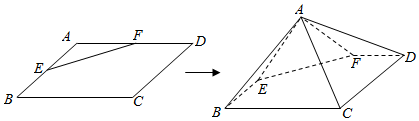
15.四棱锥P-ABCD中,PA⊥平面ABCD,∠BAD=90°,PA=AB=BC=$\frac{1}{2}$AD=1,BC∥AD,已知Q为四边形ABCD内部一点,且二面角Q-PD-A的平面角大小为$\frac{π}{4}$,若动点Q的轨迹将四边形ABCD分成面积为S1,S2(S1<S2)的两部分,则S1:S2=(3$\sqrt{5}$-4):4.分析 建立空间坐标系,求出平面PAD和平面PQD的法向量$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$,令cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$>=$\frac{\sqrt{2}}{2}$解出Q的轨迹与y轴的交点坐标,求出S1,S2得出比值.
解答 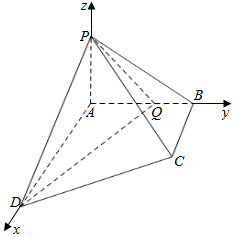 解:以A为坐标原点建立空间直角坐标系,如图:
解:以A为坐标原点建立空间直角坐标系,如图:
设Q的轨迹与y轴的交点坐标为Q(0,b,0)(b>0).
由题意可知A(0,0,0),D(2,0,0),P(0,0,1),
∴$\overrightarrow{DP}$=(-2,0,1),$\overrightarrow{DQ}$=(-2,b,0).$\overrightarrow{AD}$=(2,0,0).
设平面APD的法向量为$\overrightarrow{{n}_{1}}$=(x1,y1,z1),平面PDQ的法向量为$\overrightarrow{{n}_{2}}$=(x2,y2,z2)
则$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{DP}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{AD}=0}\end{array}\right.$,$\left\{\begin{array}{l}{\overrightarrow{{n}_{2}}•\overrightarrow{DP}=0}\\{\overrightarrow{{n}_{2}}•\overrightarrow{DQ}=0}\end{array}\right.$.
即$\left\{\begin{array}{l}{-2{x}_{1}+{z}_{1}=0}\\{2{x}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{-2{x}_{2}+{z}_{2}=0}\\{-2{x}_{2}+b{y}_{2}=0}\end{array}\right.$,
令y1=0得$\overrightarrow{{n}_{1}}$=(0,1,0),令z2=2得$\overrightarrow{{n}_{2}}$=(1,$\frac{2}{b}$,2).
∴$\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}$=$\frac{2}{b}$,$|\overrightarrow{{n}_{1}}|=1$,$|\overrightarrow{{n}_{2}}|=\sqrt{5+\frac{4}{{b}^{2}}}$.
∵二面角Q-PD-A的平面角大小为$\frac{π}{4}$,
∴cos<$\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}$>=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$\frac{\sqrt{2}}{2}$.即$\frac{\frac{2}{b}}{\sqrt{5+\frac{4}{{b}^{2}}}}=\frac{\sqrt{2}}{2}$,解得b=$\frac{2\sqrt{5}}{5}$.
∴S△ADQ=$\frac{1}{2}AD•AQ$=$\frac{1}{2}×2×\frac{2\sqrt{5}}{5}=\frac{2\sqrt{5}}{5}$.
S梯形ABCD-S△ADQ=$\frac{1}{2}×(1+2)×1$-$\frac{2\sqrt{5}}{5}$=$\frac{3}{2}-\frac{2\sqrt{5}}{5}$.
∵S1<S2,∴S1=$\frac{3}{2}$-$\frac{2\sqrt{5}}{5}$,S2=$\frac{2\sqrt{5}}{5}$.
∴S1:S2=(3$\sqrt{5}$-4):4.
故答案为(3$\sqrt{5}$-4):4.
点评 本题考查了二面角的计算,使用向量可比较方便的找到Q的轨迹.属于中档题.

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案| A. | “a≤b”是“a+c≤b+c”的必要不充分条件 | |
| B. | 如果空间两条直线不相交,则这两条直线平行 | |
| C. | 设命题p:?x∈R,x2+1>0,则¬p为?x0∈R,x02+1<0 | |
| D. | “若α=$\frac{π}{4}$,则tanα=1”的逆否命题为“若tanα≠1,则α≠$\frac{π}{4}$” |
| A. | 16 | B. | 8 | C. | 16或32 | D. | 16或8 |
| A. | 1-cos1 | B. | 1-sin1 | C. | $\frac{π}{2}$ | D. | -$\frac{π}{2}$ |