$\underset{lim}{n→∞}$$\sum {i=1}^{n}$($\frac{1}{n}$sin$\frac{i}{n}$)=( )A．1-cos1B．1-sin1C．$\frac{π}{2}$D．-$\frac{π}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

4．$\underset{lim}{n→∞}$$\sum_{i=1}^{n}$（$\frac{1}{n}$sin$\frac{i}{n}$）=（　　）

A．

1-cos1

B．

1-sin1

C．

$\frac{π}{2}$

D．

-$\frac{π}{2}$

分析利用定积分的性质将其化简为）${∫}_{0}^{1}sinxdx$=1-cos1．

解答解$\underset{lim}{n→∞}$$\sum_{i=1}^{n}$（$\frac{1}{n}$sin$\frac{i}{n}$）=${∫}_{0}^{1}sinxdx$，
=-cosx${丨}_{0}^{1}$，
=1-cos1．
故答案选：A．

点评本题考查定积分的定义及运算，属于基础题．

练习册系列答案

15．四棱锥P-ABCD中，PA⊥平面ABCD，∠BAD=90°，PA=AB=BC=$\frac{1}{2}$AD=1，BC∥AD，已知Q为四边形ABCD内部一点，且二面角Q-PD-A的平面角大小为$\frac{π}{4}$，若动点Q的轨迹将四边形ABCD分成面积为S₁，S₂（S₁＜S₂）的两部分，则S₁：S₂=（3$\sqrt{5}$-4）：4．

12．已知$\overrightarrow{OA}$=（-1，3），$\overrightarrow{OB}$=（3，-1），$\overrightarrow{OC}$=（m，1）
（1）若$\overrightarrow{AB}$∥$\overrightarrow{OC}$，求实数m的值；
（2）若$\overrightarrow{AC}$⊥$\overrightarrow{BC}$，求实数m的值．

19．

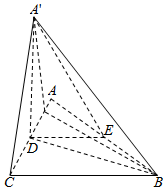如图，△ABC是等腰直角三角形，∠ACB=90°，AC=2a，D，E分别为AC，AB的中点，沿DE将△ADE折起，得到四棱锥A′-BCDE，已知A′H⊥CD，垂足为H．
（Ⅰ）求证：平面A′HB⊥平面BCDE；
（Ⅱ）求三棱锥B-A′DE的最大体积．

9．若集合A={1，m²}，B={3，4}，则“m=2”是“A∩B={4}”的充分不必要条件．（填“充分不必要条件”、“必要不充分条件”、“充分必要条件”、“既不充分也不必要条件”中的一个）

16．已知k∈Z，角的终边只落在y轴正半轴上的角是（　　）

13．

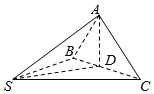如图所示，在四面体S-ABC中，SA=SB=SC=1，∠ASB=∠ASC=60°，∠BSC=90°，D是BC的中点．求证：
（1）SD⊥平面ABC；
（2）AD⊥SC；
（3）BC⊥SA．

14．若圆C₁：x²+y²+ax=0与圆C₂：x²+y²+2ax+ytanθ=0都关于直线2x-y-1=0对称，则sinθcosθ=（　　）

试题分类