题目内容
10.下列命题中,真命题是( )| A. | “a≤b”是“a+c≤b+c”的必要不充分条件 | |
| B. | 如果空间两条直线不相交,则这两条直线平行 | |
| C. | 设命题p:?x∈R,x2+1>0,则¬p为?x0∈R,x02+1<0 | |
| D. | “若α=$\frac{π}{4}$,则tanα=1”的逆否命题为“若tanα≠1,则α≠$\frac{π}{4}$” |
分析 A.根据充分条件和必要条件的定义进行判断
B.根据空间直线的位置关系进行判断
C.根据含有量词的命题的否定进行判断
D.根据逆否命题的定义进行判断.
解答 解:A.“a≤b”等价于“a+c≤b+c”,则“a≤b”是“a+c≤b+c”的充要条件,故A错误,
B.如果空间两条直线不相交,则这两条直线平行或异面.故B错误,
C.命题p:?x∈R,x2+1>0,则¬p为?x0∈R,x02+1≤0,故C错误,
D.若α=$\frac{π}{4}$,则tanα=1”的逆否命题为“若tanα≠1,则α≠$\frac{π}{4}$”正确,
故选:D.
点评 本题主要考查命题的真假判断,涉及充分条件和必要条件,逆否命题的定义以及含有量词的命题的否定,涉及的知识点较多,综合性较强,但难度不大.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
20.设集合A={x|$\frac{\sqrt{2}}{2}$≤2x≤$\sqrt{2}}\right\}$,B={x|lnx<0},则A∩B=( )
| A. | (-$\frac{1}{2}$,$\frac{1}{2}$) | B. | (0,$\frac{1}{2}$) | C. | [$\frac{1}{2}$,1) | D. | (0,$\frac{1}{2}$] |
1.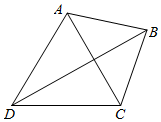 某学习小组进行课外研究性学习,为了测量如图所示不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小分别为∠ADB=30°,∠CDB=30°,∠ACD=60°,∠ACB=45°,则A、B两地的距离大约等于( )(提供数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$,结果保留两个有效数字)
某学习小组进行课外研究性学习,为了测量如图所示不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小分别为∠ADB=30°,∠CDB=30°,∠ACD=60°,∠ACB=45°,则A、B两地的距离大约等于( )(提供数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$,结果保留两个有效数字)
 某学习小组进行课外研究性学习,为了测量如图所示不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小分别为∠ADB=30°,∠CDB=30°,∠ACD=60°,∠ACB=45°,则A、B两地的距离大约等于( )(提供数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$,结果保留两个有效数字)
某学习小组进行课外研究性学习,为了测量如图所示不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小分别为∠ADB=30°,∠CDB=30°,∠ACD=60°,∠ACB=45°,则A、B两地的距离大约等于( )(提供数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$,结果保留两个有效数字)| A. | 1.3 | B. | 1.4 | C. | 1.5 | D. | 1.6 |
5.已知数列{an}满足a1=1,an-an-1=n(n≥2),则数列{an}的通项公式an=( )
| A. | $\frac{1}{2}n(n+1)$ | B. | $\frac{1}{2}n(3n-1)$ | C. | n2-n+1 | D. | n2-2n+2 |
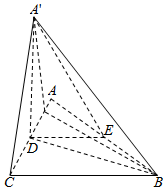 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到四棱锥A′-BCDE,已知A′H⊥CD,垂足为H.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到四棱锥A′-BCDE,已知A′H⊥CD,垂足为H.