题目内容
7.如图菱形ABCD的边长为4,E,F分别为AB,AD的中点,∠BAD=120°,沿EF将平面AEF折起形成一个五棱锥A-BCDFE.(1)证明:EF⊥AC;
(2)当翻折形成的五棱锥体积最大时,取CD中点M,求二面角M-AE-F的余弦值.
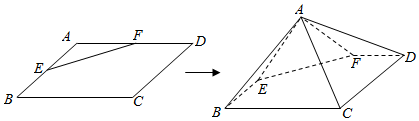
分析 (1)根据线面垂直的判定定理证明EF⊥平面AHC即可.
(3)当翻折形成的五棱锥体积最大时,即AH⊥平面BCDE,建立坐标系求出平面的法向量,利用向量法即可求二面角M-AE-F的余弦值.
解答 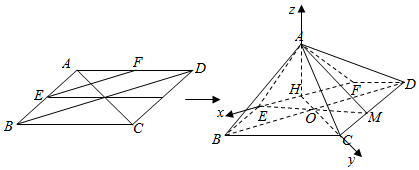 (1)证明:连接AC交BC于O,交EF于H,
(1)证明:连接AC交BC于O,交EF于H,
∵ABCD是菱形,
∴EF⊥AH,EF⊥HC,
∵AH∩HC=H,
∴EF⊥平面AHC,
∵AC?平面AHC,
∴EF⊥AC;
(2)当翻折形成的五棱锥体积最大时,则五棱锥的高最大即可,
即AH⊥平面BCDE,建立以H为坐标原点,HE,HC,HA分别为x,y,z轴的空间直角坐标系如图:
∵菱形ABCD的边长为4,E,F分别为AB,AD的中点,∠BAD=120°,
∴H(0,0,0)A(0,0,1),E($\sqrt{3}$,0,0),F(-$\sqrt{3}$,0,0),C(0,3,0),M(-$\sqrt{3}$,2,0),
$\overrightarrow{AE}$=($\sqrt{3}$,0,-1),$\overrightarrow{EM}$=(-2$\sqrt{3}$,2,0),$\overrightarrow{AF}$=(-$\sqrt{3}$,0,-1),
则平面AEF的法向量$\overrightarrow{m}$=(0,1,0),
设平面MAE的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AE}=0}\\{\overrightarrow{n}•\overrightarrow{EM}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{\sqrt{3}x-z=0}\\{-2\sqrt{3}x+2y=0}\end{array}\right.$,令x=$\sqrt{3}$,则y=z=3,
即$\overrightarrow{n}$=($\sqrt{3}$,3,3),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{3}{\sqrt{3+9+9}}=\frac{3}{\sqrt{21}}$=$\frac{\sqrt{21}}{7}$,
即二面角M-AE-F的余弦值是$\frac{\sqrt{21}}{7}$.
点评 本题主要考查线面垂直的性质以及二面角的求解,建立空间直角坐标系,利用向量法进行求解,综合性较强,运算量较大.

| A. | $\frac{kπ}{2}$ | B. | kπ+$\frac{π}{2}$ | C. | 2kπ+$\frac{π}{2}$ | D. | 2kπ-$\frac{π}{2}$ |
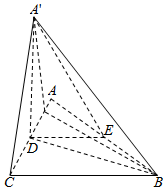 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到四棱锥A′-BCDE,已知A′H⊥CD,垂足为H.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到四棱锥A′-BCDE,已知A′H⊥CD,垂足为H.