题目内容
6.已知tanα=-3,求下列各式的值:(1)$\frac{sinα-3cosα}{sinα+cosα}$;
(2)sin2α+sinαcosα+2.
分析 由条件利用同角三角函数的基本关系,求得要求式子的值.
解答 解:(1)∵tanα=-3,
∴$\frac{sinα-3cosα}{sinα+cosα}=\frac{tanα-3}{tanα+1}=3$.
(2)sin2α+sinαcosα+2=$\frac{{{{sin}^2}α+sinαcosα}}{{{{sin}^2}α+{{cos}^2}α}}+2$=$\frac{{{{tan}^2}α+tanα}}{{{{tan}^2}α+1}}+2$=$\frac{13}{5}$.
点评 本题主要考查同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
相关题目
14.若数列$\sqrt{2}$,$\sqrt{5}$,$2\sqrt{2}$,$\sqrt{11}$,$\sqrt{14}$,…,则$4\sqrt{2}$是这个数列的第( )项.
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
1.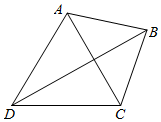 某学习小组进行课外研究性学习,为了测量如图所示不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小分别为∠ADB=30°,∠CDB=30°,∠ACD=60°,∠ACB=45°,则A、B两地的距离大约等于( )(提供数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$,结果保留两个有效数字)
某学习小组进行课外研究性学习,为了测量如图所示不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小分别为∠ADB=30°,∠CDB=30°,∠ACD=60°,∠ACB=45°,则A、B两地的距离大约等于( )(提供数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$,结果保留两个有效数字)
 某学习小组进行课外研究性学习,为了测量如图所示不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小分别为∠ADB=30°,∠CDB=30°,∠ACD=60°,∠ACB=45°,则A、B两地的距离大约等于( )(提供数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$,结果保留两个有效数字)
某学习小组进行课外研究性学习,为了测量如图所示不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小分别为∠ADB=30°,∠CDB=30°,∠ACD=60°,∠ACB=45°,则A、B两地的距离大约等于( )(提供数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$,结果保留两个有效数字)| A. | 1.3 | B. | 1.4 | C. | 1.5 | D. | 1.6 |
11.随着国民生活水平的提高,利用长假旅游的人越来越多.某公司统计了2012到2016年五年间本公司职员每年春节期间外出旅游的家庭数,具体统计数据如表所示:
(Ⅰ)从这5年中随机抽取两年,求外出旅游的家庭数至少有1年多于20个的概率;
(Ⅱ)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程$\hat y=\hat bx+\hat a$,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 年份(x) | 2012 | 2013 | 2014 | 2015 | 2016 |
| 家庭数(y) | 6 | 10 | 16 | 22 | 26 |
(Ⅱ)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程$\hat y=\hat bx+\hat a$,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
16.已知k∈Z,角的终边只落在y轴正半轴上的角是( )
| A. | $\frac{kπ}{2}$ | B. | kπ+$\frac{π}{2}$ | C. | 2kπ+$\frac{π}{2}$ | D. | 2kπ-$\frac{π}{2}$ |
 如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.
如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.