题目内容
已知函数f(x)=2x,若对于实数a,b,c有f(a+b)=f(a)+f(b),f(a+b+c)=f(a)+f(b)+3f(c),则实数c的值为 .
考点:抽象函数及其应用,函数的值
专题:计算题,函数的性质及应用
分析:由题意得,2a+b=2a+2b;2a+b+c=2a+2b+3•2c,利用换元法令2a=M>0,2b=N>0,从而求得MN≥4,(当且仅当M=N=2时,等号成立);再化简2c=
=
=
≤4,从而求C.
| M+N |
| MN-3 |
| MN |
| MN-3 |
| 1 | ||
1-
|
解答:
解:由题意得,
2a+b=2a+2b;
2a+b+c=2a+2b+3•2c,
令2a=M>0,2b=N>0,
则2a+b=2a+2b可化为
MN=M+N≥2
,
MN≥4,(当且仅当M=N=2时,等号成立);
2a+b+c=2a+2b+3•2c可化为
MN2c=M+N+3•2c,
则2c=
=
=
≤4;
(当且仅当M=N=2时,等号成立)
故实数c的最大值为2;
故答案为:2.
2a+b=2a+2b;
2a+b+c=2a+2b+3•2c,
令2a=M>0,2b=N>0,
则2a+b=2a+2b可化为
MN=M+N≥2
| MN |
MN≥4,(当且仅当M=N=2时,等号成立);
2a+b+c=2a+2b+3•2c可化为
MN2c=M+N+3•2c,
则2c=
| M+N |
| MN-3 |
| MN |
| MN-3 |
| 1 | ||
1-
|
(当且仅当M=N=2时,等号成立)
故实数c的最大值为2;
故答案为:2.
点评:本题考查了函数的应用及换元法的应用,同时考查了基本不等式的应用,属于中档题.

练习册系列答案
相关题目
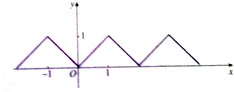 已知函数y=f(x)的图象如图所示,试回答下列问题:
已知函数y=f(x)的图象如图所示,试回答下列问题: