题目内容
三棱柱的底面是边长为4的正三角形,侧棱长为3,一条侧棱与底面相邻两边都成60°角,求此棱柱的侧面积与体积.
考点:棱柱、棱锥、棱台的体积,棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:过A1作A1O⊥底面ABC交底面于O,过A1作A1E⊥AB交AB于E,过A1作A1F⊥AC交AC于F,连结EO、FO,由三垂线定理得EO⊥AB,FO⊥AC.由此能求出此棱柱的侧面积与体积.
解答:
 解:如图,过A1作A1O⊥底面ABC交底面于O,
解:如图,过A1作A1O⊥底面ABC交底面于O,
过A1作A1E⊥AB交AB于E,过A1作A1F⊥AC交AC于F,
连结EO、FO,由三垂线定理得EO⊥AB,FO⊥AC.?
∵AA1和AB与AC都成60°角,?
∴△A1AE≌△A1AF.∴A1E=A1F.?
∵A1O⊥底面ABC,∴EO=FO.?
∴点O在∠BAC的角平分线上.?
延长AO交BC于点D,?
∵△ABC是正三角形,∴BC⊥AD.∴BC⊥AA1.?
∵AA1∥BB1,∴侧面BB1C1C是矩形.?
∴三棱柱的侧面积为?
S=2×
×3×4×sin60°+3×4=12+6
.?
∵AA1=3,AA1和AB与AC都成60°角,
∴AE=
.?
∵∠BAO=30°,∴AO=
,A1O=
.?
∴三棱柱的体积为V=
×
×16×
=4
.
 解:如图,过A1作A1O⊥底面ABC交底面于O,
解:如图,过A1作A1O⊥底面ABC交底面于O,过A1作A1E⊥AB交AB于E,过A1作A1F⊥AC交AC于F,
连结EO、FO,由三垂线定理得EO⊥AB,FO⊥AC.?
∵AA1和AB与AC都成60°角,?
∴△A1AE≌△A1AF.∴A1E=A1F.?
∵A1O⊥底面ABC,∴EO=FO.?
∴点O在∠BAC的角平分线上.?
延长AO交BC于点D,?
∵△ABC是正三角形,∴BC⊥AD.∴BC⊥AA1.?
∵AA1∥BB1,∴侧面BB1C1C是矩形.?
∴三棱柱的侧面积为?
S=2×
| 1 |
| 2 |
| 3 |
∵AA1=3,AA1和AB与AC都成60°角,
∴AE=
| 3 |
| 2 |
∵∠BAO=30°,∴AO=
| 3 |
| 6 |
∴三棱柱的体积为V=
| 1 |
| 3 |
| ||
| 4 |
| 6 |
| 2 |
点评:本题考查棱柱的侧面积与体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
设函数f(x)在(0,+∞)上是增函数,a=f(2
),b=f(log2
)的大小( )
| 3 |
| 2 |
| 3 |
| 2 |
| A、a>b | B、a<b |
| C、a≥b | D、a≤b |
已知数列{an}的前n项和Sn=n2+n+1,则a1+a9等于( )
| A、19 | B、20 | C、21 | D、22 |
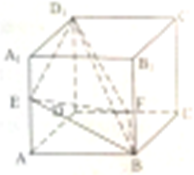 如图,已知正方体ABCD-A1B1C1D1棱长为1,E,F分别为AA1,CD的中点,则四面体D1EBF的体积为
如图,已知正方体ABCD-A1B1C1D1棱长为1,E,F分别为AA1,CD的中点,则四面体D1EBF的体积为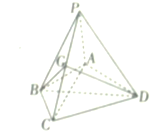 如图,在四棱锥P-ABCD中,BD⊥PC,AB=BC=2,AD=CD=
如图,在四棱锥P-ABCD中,BD⊥PC,AB=BC=2,AD=CD=