题目内容
9.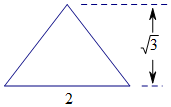 一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )
一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $\frac{8}{3}$ |
分析 由题意该四棱锥是底面边长为2,高为$\sqrt{3}$的正四棱锥,由此能求出该四棱锥的体积.
解答 解: 由题意该四棱锥是底面边长为2,高为$\sqrt{3}$的正四棱锥,
由题意该四棱锥是底面边长为2,高为$\sqrt{3}$的正四棱锥,
即四棱锥S-ABCD中,底面ABCD是边长为2的正方形,
SO⊥平面ABCD,O是正方形ABCD的中心,且SO=$\sqrt{3}$,
∴该四棱锥的体积:
V=$\frac{1}{3}×{S}_{正方形ABCD}×SO$=$\frac{1}{3}×{2}^{2}×\sqrt{3}$=$\frac{4\sqrt{3}}{3}$.
故选:A.
点评 本题考查四棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系的合理运用,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,考查创新意识、应用意识,是中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
19.数列{an}中,${a_{n+1}}+{(-1)^n}{a_n}=2n-1$,则数列{an}前16项和等于( )
| A. | 130 | B. | 132 | C. | 134 | D. | 136 |
17.已知点P为函数f(x)=lnx的图象上任意一点,点Q为圆${[{x-(e+\frac{1}{e})}]^2}+{y^2}=\frac{1}{4}$上任意一点,则线段PQ长度的最小值为( )
| A. | $\frac{{e-\sqrt{{e^2}-1}}}{e}$ | B. | $\frac{{2\sqrt{{e^2}+1}-e}}{2e}$ | C. | $\frac{{\sqrt{{e^2}+1}-e}}{2e}$ | D. | $e+\frac{1}{e}-\frac{1}{2}$ |
1.设变量x,y满足$\left\{\begin{array}{l}{2x+y-6≥0}\\{x+2y-6≥0}\\{y≥0}\end{array}\right.$,则目标函数z=2x+3y的最小值为( )
| A. | 6 | B. | 10 | C. | 12 | D. | 18 |
18.已知复数z=a+$\sqrt{3}$i(a∈R)在复平面内对应的点位于第二象限,且|z|=2,则复数z等于( )
| A. | -1+$\sqrt{3}$i | B. | 1+$\sqrt{3}$i | C. | -1+$\sqrt{3}$i或1+$\sqrt{3}$i | D. | -2+$\sqrt{3}$i |