题目内容
1．设变量x，y满足$\left\{\begin{array}{l}{2x+y-6≥0}\\{x+2y-6≥0}\\{y≥0}\end{array}\right.$，则目标函数z=2x+3y的最小值为（ ）| A． | 6 | B． | 10 | C． | 12 | D． | 18 |
分析 画出可行域表示的平面区域，找出最优解，求出目标函数的最小值．
解答 解：画出可行域$\left\{\begin{array}{l}{2x+y-6≥0}\\{x+2y-6≥0}\\{y≥0}\end{array}\right.$表示的平面区域，如图所示；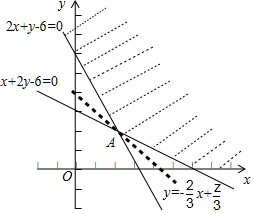
由$\left\{\begin{array}{l}{2x+y-6=0}\\{x+2y-6=0}\end{array}\right.$求得点A（2，2），
目标函数z=2x+3y化为y=-$\frac{2}{3}$x+$\frac{z}{3}$；
当目标函数过点A时，z取得最小值为
zmin=2×2+3×2=10．
故选：B．
点评 本题考查了简单的线性规划的应用问题，也考查了数形结合的应用问题，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
11．函数f（x）=sin（2x+$\frac{π}{6}$）的最小正周期为（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | 2π | D． | 4π |
9．
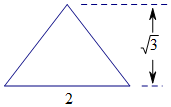一个四棱锥的侧棱长都相等，底面是正方形，且其正视图为如图所示的等腰三角形，则该四棱锥的体积是（ ）
一个四棱锥的侧棱长都相等，底面是正方形，且其正视图为如图所示的等腰三角形，则该四棱锥的体积是（ ）| A． | $\frac{{4\sqrt{3}}}{3}$ | B． | $2\sqrt{3}$ | C． | $4\sqrt{3}$ | D． | $\frac{8}{3}$ |
6．下列各函数中，最小值为4的是（ ）
| A． | $y=x+\frac{4}{x}$ | B． | $y=sinx+\frac{4}{sinx}（0＜x＜π）$ | ||
| C． | y=4log3x+logx3 | D． | y=4ex+e-x |
13．不等式（m+1）x2-mx+m-1＜0的解集为∅，则m的取值范围（ ）
| A． | m＜-1 | B． | m≥$\frac{2\sqrt{3}}{3}$ | C． | m≤-$\frac{2\sqrt{3}}{3}$ | D． | m≥$\frac{2\sqrt{3}}{3}$或m≤-$\frac{2\sqrt{3}}{3}$ |
10．已知抛物线y2=12x，则该抛物线的准线方程为（ ）
| A． | x=-3 | B． | x=3 | C． | y=-3 | D． | y=3 |