题目内容
19.数列{an}中,${a_{n+1}}+{(-1)^n}{a_n}=2n-1$,则数列{an}前16项和等于( )| A. | 130 | B. | 132 | C. | 134 | D. | 136 |
分析 an+1+(-1)n an=2n-1,可得a2-a1=1,a3+a2=3,a4-a3=5,a5+a4=7,a6-a5=9,a7+a6=11,…a16-a15=29.
从而可得a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,a9+a11=2,a12+a10=40,a13+a15=2,a16+a14=56,即可得出.
解答 解:∵an+1+(-1)n an=2n-1,
∴a2-a1=1,a3+a2=3,a4-a3=5,a5+a4=7,a6-a5=9,a7+a6=11,…a16-a15=29.
从而可得a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,a9+a11=2,a12+a10=40,a13+a15=2,a16+a14=56,
从第一项开始,依次取2个相邻奇数项的和都等于2,从第二项开始,
依次取2个相邻偶数项的和构成以8为首项,以16为公差的等差数列.
∴{an}的前16项和为 4×2+8×4+$\frac{4×3}{2}×16$=136.
故选:D.
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
7.己知三棱锥A-BCO,OA,OB,OC两两垂直且长度均为6,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在底面BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的O点所在的三个面所围成的几何体的表面积为( )
| A. | $\frac{5π}{2}$ | B. | $\frac{5π}{4}$ | C. | $\frac{3+π}{2}$ | D. | 3+π |
11.函数f(x)=sin(2x+$\frac{π}{6}$)的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
8.下列函数中,既是奇函数又存在零点的是( )
| A. | y=sinx | B. | y=lnx | C. | y=x2 | D. | y=$\frac{1}{x}$ |
9.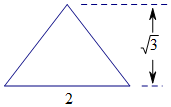 一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )
一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )
 一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )
一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $\frac{8}{3}$ |