题目内容
14.下列说法:①正切函数y=tanx在定义域内是增函数;
②函数$f(x)=cos(\frac{2}{3}x+\frac{π}{2})$是奇函数;
③$x=\frac{π}{8}$是函数$y=sin(2x+\frac{5}{4}π)$的一条对称轴方程;
其中正确的是??②③.(写出所有正确答案的序号)
分析 ①,正切函数y=tanx在(kπ-$\frac{π}{2}$,kπ+$\frac{π}{2}$)k∈Z内是增函数;
②,函数f(x)=cos($\frac{2}{3}$x+$\frac{π}{2}$)=-sin$\frac{2}{3}$x在判断;
③,验证当x=$\frac{π}{8}$时,函数f(x)=sin(2x+$\frac{5π}{4}$)是否取最值;
解答 解:对于①,正切函数y=tanx在(kπ-$\frac{π}{2}$,kπ+$\frac{π}{2}$)k∈Z内是增函数,故错;
对于②,函数f(x)=cos($\frac{2}{3}$x+$\frac{π}{2}$)=-sin$\frac{2}{3}$x是奇函数,故正确;
对于③,∵当x=$\frac{π}{8}$时函数f(x)=sin(2x+$\frac{5π}{4}$)取得最小值,故正确;
故答案为:②③.
点评 本题考查了命题真假的判定,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列描述不能看作算法的是( )
| A. | 做米饭需要刷锅,淘米,添水,加热这些步骤 | |
| B. | 洗衣机的使用说明书 | |
| C. | 利用公式S=πr2计算半径为4的圆的面积,就是计算π×42 | |
| D. | 解方程2x2+x-1=0 |
9.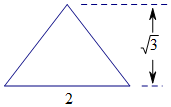 一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )
一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )
 一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )
一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $\frac{8}{3}$ |
19.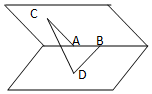 如图在一个60°的二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,且AB=AC=1,BD=2,则CD的长为( )
如图在一个60°的二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,且AB=AC=1,BD=2,则CD的长为( )
 如图在一个60°的二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,且AB=AC=1,BD=2,则CD的长为( )
如图在一个60°的二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,且AB=AC=1,BD=2,则CD的长为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | 1 |
6.下列各函数中,最小值为4的是( )
| A. | $y=x+\frac{4}{x}$ | B. | $y=sinx+\frac{4}{sinx}(0<x<π)$ | ||
| C. | y=4log3x+logx3 | D. | y=4ex+e-x |
3.若抛物线y2=2px的焦点与双曲线$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{1}$=1的右焦点重合,则p的值为( )
| A. | 2$\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2 |
4.已知$\vec a=(x,4),\vec b=(3,2)$,$\vec a∥\vec b,则x$=( )
| A. | -6 | B. | $-\frac{3}{8}$ | C. | 6 | D. | $\frac{3}{8}$ |