题目内容
18.已知复数z=a+$\sqrt{3}$i(a∈R)在复平面内对应的点位于第二象限,且|z|=2,则复数z等于( )| A. | -1+$\sqrt{3}$i | B. | 1+$\sqrt{3}$i | C. | -1+$\sqrt{3}$i或1+$\sqrt{3}$i | D. | -2+$\sqrt{3}$i |
分析 由题意可得:$\left\{\begin{array}{l}{a<0}\\{\sqrt{{a}^{2}+3}=2}\end{array}\right.$,解得a,即可得出.
解答 解:复数z=a+$\sqrt{3}$i(a∈R)在复平面内对应的点位于第二象限,且|z|=2,
∴$\left\{\begin{array}{l}{a<0}\\{\sqrt{{a}^{2}+3}=2}\end{array}\right.$,解得a=-1.
则复数z=-1+$\sqrt{3}$i.
故选:A.
点评 本题考查了复数的运算法则、模的计算公式、几何意义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列函数中,既是奇函数又存在零点的是( )
| A. | y=sinx | B. | y=lnx | C. | y=x2 | D. | y=$\frac{1}{x}$ |
9.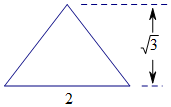 一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )
一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )
 一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )
一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $\frac{8}{3}$ |
6.下列各函数中,最小值为4的是( )
| A. | $y=x+\frac{4}{x}$ | B. | $y=sinx+\frac{4}{sinx}(0<x<π)$ | ||
| C. | y=4log3x+logx3 | D. | y=4ex+e-x |
13.不等式(m+1)x2-mx+m-1<0的解集为∅,则m的取值范围( )
| A. | m<-1 | B. | m≥$\frac{2\sqrt{3}}{3}$ | C. | m≤-$\frac{2\sqrt{3}}{3}$ | D. | m≥$\frac{2\sqrt{3}}{3}$或m≤-$\frac{2\sqrt{3}}{3}$ |
3.若抛物线y2=2px的焦点与双曲线$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{1}$=1的右焦点重合,则p的值为( )
| A. | 2$\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2 |
10.已知抛物线y2=12x,则该抛物线的准线方程为( )
| A. | x=-3 | B. | x=3 | C. | y=-3 | D. | y=3 |