题目内容
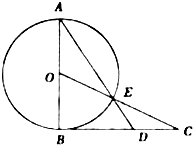 如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.
如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.(1)求证:CE2=CD•CB;
(2)若AB=BC=2,求CE和CD的长.
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:(1)要证CE2=CD•CB,结合题意,只需证明△CED∽△CBE即可,故连接BE,利用弦切角的知识即可得证;
(2)在Rt三△OBC中,利用勾股定理即可得出CE的长,由(1)知,CE2=CD•CB,代入CE即可得出CD的长.
(2)在Rt三△OBC中,利用勾股定理即可得出CE的长,由(1)知,CE2=CD•CB,代入CE即可得出CD的长.
解答:
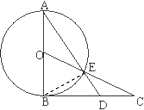 (1)证明:连接BE.
(1)证明:连接BE.
∵BC为⊙O的切线∴∠ABC=90°
∵AB为⊙O的直径∴∠AEB=90° …(2分)
∴∠DBE+∠OBE=90°,∠AEO+∠OEB=90°
∵OB=OE,∴∠OBE=∠OEB∴∠DBE=∠AEO …(4分)
∵∠AEO=∠CED∴∠CED=∠CBE,
∵∠C=∠C∴△CED∽△CBE,
∴
=
,∴CE2=CD•CB …(6分)
(2)解:∵OB=1,BC=2,∴OC=
,∴CE=OC-OE=
-1 …(8分)
由(1)CE2=CD•CB得:(
-1)2=2CD,∴CD=3-
…(10分)
 (1)证明:连接BE.
(1)证明:连接BE.∵BC为⊙O的切线∴∠ABC=90°
∵AB为⊙O的直径∴∠AEB=90° …(2分)
∴∠DBE+∠OBE=90°,∠AEO+∠OEB=90°
∵OB=OE,∴∠OBE=∠OEB∴∠DBE=∠AEO …(4分)
∵∠AEO=∠CED∴∠CED=∠CBE,
∵∠C=∠C∴△CED∽△CBE,
∴
| CE |
| CB |
| CD |
| CE |
(2)解:∵OB=1,BC=2,∴OC=
| 5 |
| 5 |
由(1)CE2=CD•CB得:(
| 5 |
| 5 |
点评:本题主要考查了切线的性质及其应用,同时考查了相似三角形的判定和解直角三角形等知识点,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
抛物线y=
x2的焦点坐标为( )
| 1 |
| 8 |
| A、(0,2) | ||
B、(0,
| ||
| C、(2,0) | ||
D、(
|
若函数y=
的定义域为R,则实数m的取值范围是( )
| m(x+1)-2 | |||
|
A、(0,
| ||
B、(0,
| ||
C、[0,
| ||
D、[0,
|
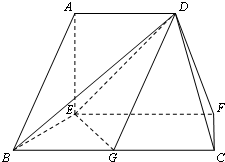 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,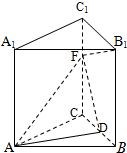 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是C1C上一点,且CF=2a.
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是C1C上一点,且CF=2a. 已知:如图AD,BC,AE分别是⊙O的三条切线,切点分别是D,E,F,AG是⊙O的一条割线,交⊙O于F,G两点,△ABC的周长2
已知:如图AD,BC,AE分别是⊙O的三条切线,切点分别是D,E,F,AG是⊙O的一条割线,交⊙O于F,G两点,△ABC的周长2 如图,四棱锥A-BCDE,平面ABC⊥平面BCDE,△ABC边长为2的等边三角形,底面BCDE是矩形,且CD=
如图,四棱锥A-BCDE,平面ABC⊥平面BCDE,△ABC边长为2的等边三角形,底面BCDE是矩形,且CD=