题目内容
如图，在△ABC中，AB=4，AC=1，∠BAC=60°．（1）求BC的长和sin∠ACB的值；
（2）延长AB到M，延长AC到N，连结MN，若四边形BMNC的面积为3
| 3 |
| BM |
| CN |
考点：平面向量数量积的运算,正弦定理,余弦定理
专题：平面向量及应用
分析：对第（1）问，已知两边和这两边的夹角，考虑用余弦定理，再用正弦定理求sin∠ACB的值；
对第（2）问，利用三角形面积公式“S=
absinC”，将四边形BMNC的面积转化为△AMN的面积与△ABC的面积之差，从而建立方程，得到|
||
|及
•
的值，将
•
用|
|，|
|表示，再探求其最大值．
对第（2）问，利用三角形面积公式“S=
| 1 |
| 2 |
| AM |
| AN |
| AM |
| AN |
| BM |
| CN |
| AM |
| AN |
解答：
解：（1）由余弦定理得BC2=AB2+AC2-2AB•AC•cos∠BAC
=42+12-2×4×1×cos60°=13，
∴BC=
．
∵sin∠BAC=sin60°=
，∴由正弦定理得
=
，
即
=
，得sin∠ACB=
．
（2）S四边形BMNC=S△AMN-S△ABC=
(|
|
-|
||
|)sin∠BAC=3
，
将|
|=4，|
|=1，∠BAC=60°代入上式，得|
||
|=16，
于是
•
=|
||
|cos∠BAC=16×
=8．
又
•
=|
||
|cos∠BAC=4×1×cos60°=2，
∴
•
=(
-
)•(
-
)=
•
+
•
-(
•
+
•
)
=10-(2|
+
|
|)≤10-2
=10-2
=2，即
•
≤2，
当且仅当2|
|=
|
|，即|
|=4|
|时，联立|
||
|=16，得
时，
•
=2，
∴
•
的最大值为2．
=42+12-2×4×1×cos60°=13，
∴BC=
| 13 |
∵sin∠BAC=sin60°=
| ||
| 2 |
| BC |
| sin∠BAC |
| AB |
| sin∠ACB |
即
| ||||
|
| 4 |
| sin ∠ACB |
2
| ||
| 13 |
（2）S四边形BMNC=S△AMN-S△ABC=
| 1 |
| 2 |
| AM |
| AN |
| AB |
| AC |
| 3 |
将|
| AB |
| AC |
| AM |
| AN |
于是
| AM |
| AN |
| AM |
| AN |
| 1 |
| 2 |
又
| AB |
| AC |
| AB |
| AC |
∴
| BM |
| CN |
| AM |
| AB |
| AN |
| AC |
| AM |
| CN |
| AB |
| AC |
| AB |
| AN |
| AM |
| AC |
=10-(2|
| AN |
| 1 |
| 2 |
| AM |
2|
|
| 16 |
| BM |
| CN |
当且仅当2|
| AN |
| 1 |
| 2 |
| AM |
| AM |
| AN |
| AM |
| AN |
|
| BM |
| CN |
∴
| BM |
| CN |
点评：1．本题考查了正、余弦定理，已知两边及其中一边的对角，或已知两角及任意一边，可使用正弦定理；已知两边及这两边的夹角，或已知三边，可用余弦定理．
2．向量的数量积运算在本题中运用较为灵活，可用于求模，求夹角，还可以通过模或角与三角形面积公式联系．
3．运用基本不等式求解最值问题时，应注意“一正，二定，三相等”，尤其是取“=”号的条件．
2．向量的数量积运算在本题中运用较为灵活，可用于求模，求夹角，还可以通过模或角与三角形面积公式联系．
3．运用基本不等式求解最值问题时，应注意“一正，二定，三相等”，尤其是取“=”号的条件．
练习册系列答案
优学名师名题系列答案
相关题目
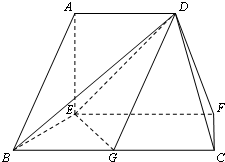在如图的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF，EF∥BC，
如图，四棱锥A-BCDE，平面ABC⊥平面BCDE，△ABC边长为2的等边三角形，底面BCDE是矩形，且CD=
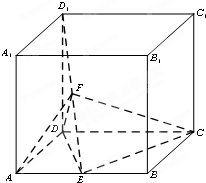如图，四棱柱ABCD-A1B1C1D1中，DD1⊥底面ABCD．ABCD为平行四边形，∠DAB=60°，AB=2AD=2．DD1=3，E，F分别是AB与D1E的中点．