题目内容
已知函数f(x)=2x3-3(a+1)x2+6ax(a∈R).
(1)若函数f(x)在(-∞,+∞)上单调递增,求实数a的取值集合;
(2)当x∈[1,3]时,f(x)的最小值为4,求实数a的值.
(1)若函数f(x)在(-∞,+∞)上单调递增,求实数a的取值集合;
(2)当x∈[1,3]时,f(x)的最小值为4,求实数a的值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1))由于函数f(x)在(-∞,+∞)上单调递增,可得f′(x)≥0恒成立,于是可得△≤0恒成立,解得即可;
(2)由(1)可得:f′(x)=6(x-1)(x-a).对a分类讨论:a≤1,1<a<3,a≥3三种情况利用导数研究函数的单调性即可得出.
(2)由(1)可得:f′(x)=6(x-1)(x-a).对a分类讨论:a≤1,1<a<3,a≥3三种情况利用导数研究函数的单调性即可得出.
解答:
解:(1)∵函数f(x)在(-∞,+∞)上单调递增,
∴f′(x)=6x2-6(a+1)x+6a=6[x2-(a+1)x+a]≥0恒成立,
∴△=(a+1)2-4a=(a-1)2≤0在R上恒成立,解得a=1.
因此实数a的取值集合为{1};
(2)由(1)可得:f′(x)=6(x-1)(x-a).
(i)当a≤1时,f′(x)≥0恒成立,且f′(x)不恒等于0,
∴f (x) 在区间[1,3]上是单调增函数,最小值为f (1).
由于f (1)=4,即2-3(a+1)+6a=4.解得a=
>1(舍去).
(ii)当1<a<3时,在区间(1,a)上f′(x)<0,∴f (x)在区间(1,a)上是减函数;
在区间(a,3)上f′(x)>0,∴f (x)在区间(a,3)上是增函数,故f (a)为最小值.
f (a)=4,即a3-3a2+4=0,解得 a=-1,a=2.
a=-1不满足条件1<a<3,应舍去.
故a=2.
(iii)当a≥3时,在区间(1,a)上f′(x)<0,∴f (x)在区间(1,a)上是减函数,f (3)为最小值.
f (3)=4,即54-27(a+1)+18a=4.解得a=
<3(舍去).
综上所述:a=2.
∴f′(x)=6x2-6(a+1)x+6a=6[x2-(a+1)x+a]≥0恒成立,
∴△=(a+1)2-4a=(a-1)2≤0在R上恒成立,解得a=1.
因此实数a的取值集合为{1};
(2)由(1)可得:f′(x)=6(x-1)(x-a).
(i)当a≤1时,f′(x)≥0恒成立,且f′(x)不恒等于0,
∴f (x) 在区间[1,3]上是单调增函数,最小值为f (1).
由于f (1)=4,即2-3(a+1)+6a=4.解得a=
| 5 |
| 3 |
(ii)当1<a<3时,在区间(1,a)上f′(x)<0,∴f (x)在区间(1,a)上是减函数;
在区间(a,3)上f′(x)>0,∴f (x)在区间(a,3)上是增函数,故f (a)为最小值.
f (a)=4,即a3-3a2+4=0,解得 a=-1,a=2.
a=-1不满足条件1<a<3,应舍去.
故a=2.
(iii)当a≥3时,在区间(1,a)上f′(x)<0,∴f (x)在区间(1,a)上是减函数,f (3)为最小值.
f (3)=4,即54-27(a+1)+18a=4.解得a=
| 23 |
| 9 |
综上所述:a=2.
点评:本题考查了利用导数研究函数的单调性极值与最值,考查了分类讨论思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
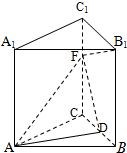 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是C1C上一点,且CF=2a.
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是C1C上一点,且CF=2a.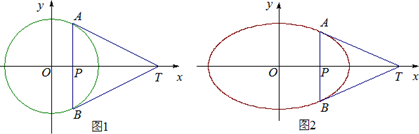
 如图,在⊙O的直径AB的延长线上任取一点C,过点C引直线与⊙O交于点D、E,在⊙O上再取一点F,使
如图,在⊙O的直径AB的延长线上任取一点C,过点C引直线与⊙O交于点D、E,在⊙O上再取一点F,使
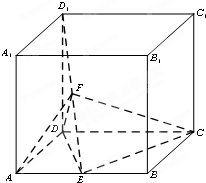 如图,四棱柱ABCD-A1B1C1D1中,DD1⊥底面ABCD.ABCD为平行四边形,∠DAB=60°,AB=2AD=2.DD1=3,E,F分别是AB与D1E的中点.
如图,四棱柱ABCD-A1B1C1D1中,DD1⊥底面ABCD.ABCD为平行四边形,∠DAB=60°,AB=2AD=2.DD1=3,E,F分别是AB与D1E的中点.