Question

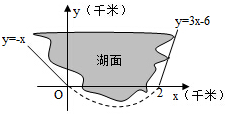如图，修建一条公路需要一段环湖弯曲路段与两条直道平滑连接（相切），已知环湖弯曲路段为某三次函数图象的一部分，则该函数的解析式为（　　）

• A、y=

  1

  2

  x³-

  1

  2

  x²-x
• B、y=

  1

  2

  x³+

  1

  2

  x²-3x
• C、y=

  1

  4

  x³-x
• D、y=

  1

  4

  x³+

  1

  2

  x²-2x

Answer 1

考点：导数的几何意义,函数解析式的求解及常用方法

专题：导数的概念及应用

分析：由题设，“需要一段环湖弯曲路段与两条直道平滑连接（相切）“可得出此两点处的切线正是两条直道所在直线，由此规律验证四个选项即可得出答案．

解答： 解：由函数图象知，此三次函数在（0，0）上处与直线y=-x相切，在（2，0）点处与y=3x-6相切，下研究四个选项中函数在两点处的切线．
A、y′=

3

2

x2-x-1，将0，2代入，解得此时切线的斜率分别是-1，3，符合题意，故A正确；
B、y′=

3

2

x2+x-3，将0代入，此时导数为-3，不为-1，故B错误；
C、y′=

3

4

x2-1，将2代入，此时导数为-1，与点（2，0）处切线斜率为3矛盾，故C错误；
D、y′=

3

4

x2+x-2，将0代入，此时导数为-2，与点（0，0）处切线斜率为-1矛盾，故D错误．
故选：A．

点评：本题考查导数的几何意义在实际问题中的应用，导数的几何意义是导数主要应用之一．