题目内容
已知等差数列{an}的公差为2,前n项和为Sn,且S1,S2,S4成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=(-1)n-1
,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=(-1)n-1
| 4n |
| anan+1 |
考点:数列的求和,数列的函数特性,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)利用等差数列与等比数列的通项公式及其前n项和公式即可得出;
(Ⅱ)由(Ⅰ)可得bn=(-1)n-1(
+
).对n分类讨论“裂项求和”即可得出.
(Ⅱ)由(Ⅰ)可得bn=(-1)n-1(
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
解:(Ⅰ)∵等差数列{an}的公差为2,前n项和为Sn,
∴Sn=na1+
d=n2-n+na1,
∵S1,S2,S4成等比数列,
∴
=S1•S4,
∴(22-2+2a1)2=a1•(42-4+4a1),化为(1+a1)2=a1(3+a1),解得a1=1.
∴an=a1+(n-1)d=1+2(n-1)=2n-1.
(Ⅱ)由(Ⅰ)可得bn=(-1)n-1
=(-1)n-1•
=(-1)n-1(
+
).
∴Tn=(1+
)-(
+
)+(
+
)+…+(-1)n-1(
+
).
当n为偶数时,Tn=(1+
)-(
+
)+(
+
)+…+(
+
)-(
+
)=1-
=
.
当n为奇数时,Tn=(1+
)-(
+
)+(
+
)+…-(
+
)+(
+
)=1+
=
.
∴Tn=
.
∴Sn=na1+
| n(n-1) |
| 2 |
∵S1,S2,S4成等比数列,
∴
| S | 2 2 |
∴(22-2+2a1)2=a1•(42-4+4a1),化为(1+a1)2=a1(3+a1),解得a1=1.
∴an=a1+(n-1)d=1+2(n-1)=2n-1.
(Ⅱ)由(Ⅰ)可得bn=(-1)n-1
| 4n |
| anan+1 |
| 4n |
| (2n-1)(2n+1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=(1+
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
当n为偶数时,Tn=(1+
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-3 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |
| 2n |
| 2n+1 |
当n为奇数时,Tn=(1+
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-3 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |
| 2n+2 |
| 2n+1 |
∴Tn=
|
点评:本题考查了等差数列与等比数列的通项公式及其前n项和公式等基础知识与基本技能方法,考查了推理能力、计算能力、“裂项求和”、分类讨论思想方法,属于难题.

练习册系列答案
相关题目
从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离不小于该正方形边长的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
阅读如图的程序框图,运行相应的程序,输出S的值为( )


| A、15 | B、105 |
| C、245 | D、945 |
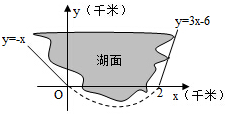 如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切),已知环湖弯曲路段为某三次函数图象的一部分,则该函数的解析式为( )
如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切),已知环湖弯曲路段为某三次函数图象的一部分,则该函数的解析式为( )A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
奇函数f(x)的定义域为R,若f(x+2)为偶函数,且f(1)=1,则f(8)+f(9)=( )
| A、-2 | B、-1 | C、0 | D、1 |
 某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300名学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300名学生每周平均体育运动时间的样本数据(单位:小时).