题目内容
在区间[-2，3]上随机选取一个数X，则X≤1的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：概率与统计
分析：利用几何槪型的概率公式，求出对应的区间长度，即可得到结论．
解答：
解：在区间[-2，3]上随机选取一个数X，
则-2≤X≤3，
则X≤1的概率P=
=
，
故选：B．
则-2≤X≤3，
则X≤1的概率P=
| 1-(-2) |
| 3-(-2) |
| 3 |
| 5 |
故选：B．
点评：本题主要考查几何槪型的概率的计算，求出对应的区间长度是解决本题的关键，比较基础．
练习册系列答案
步步高达标卷系列答案
相关题目
从正方形四个顶点及其中心这5个点中，任取2个点，则这2个点的距离不小于该正方形边长的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若将一个质点随机投入如图所示的长方形ABCD中，其中AB=2，BC=1，则质点落在以AB为直径的半圆内的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
在平面直角坐标系中，O为原点，A（-1，0），B（0，
），C（3，0），动点D满足|
|=1，则|
+
+
|的取值范围是（ ）
| 3 |
| CD |
| OA |
| OB |
| OD |
| A、[4，6] | ||||
B、[
| ||||
C、[2
| ||||
D、[
|
从正方形四个顶点及其中心这5个点中任取2个点，则这2个点的距离小于该正方形边长的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
阅读如图的程序框图，运行相应的程序，输出S的值为（ ）
| A、15 | B、105 |
| C、245 | D、945 |
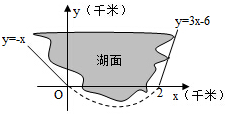如图，修建一条公路需要一段环湖弯曲路段与两条直道平滑连接（相切），已知环湖弯曲路段为某三次函数图象的一部分，则该函数的解析式为（ ）A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
某高校共有学生15000人，其中男生10500人，女生4500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300名学生每周平均体育运动时间的样本数据（单位：小时）．