题目内容
设θ为两个非零向量
,
的夹角,已知对任意实数t,|
+t
|的最小值为1.( )
| a |
| b |
| b |
| a |
A、若θ确定,则|
| ||
B、若θ确定,则|
| ||
C、若|
| ||
D、若|
|
考点:平面向量数量积的运算,零向量,数量积表示两个向量的夹角
专题:平面向量及应用
分析:由题意可得(
+t
)2=
2t2+2
•
t+
2,令g(t)=
2t2+2
•
t+
2,由二次函数可知当t=-
=-
cosθ时,g(t)取最小值1.变形可得|
|2sin2θ=1,综合选项可得结论.
| b |
| a |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
2
| ||||
2
|
|
| ||
|
|
| b |
解答:
解:由题意可得(
+t
)2=
2t2+2
•
t+
2
令g(t)=
2t2+2
•
t+
2
可得△=4(
•
)2-4
2
2=4
2
2cos2θ-4
2
2<0
由二次函数的性质可知g(t)>0恒成立
∴当t=-
=-
cosθ时,g(t)取最小值1.
即g(-
cosθ)=-|
|2cos2θ+
2=|
|2sin2θ=1
故当θ唯一确定时,|
|唯一确定,
故选:B
| b |
| a |
| a |
| a |
| b |
| b |
令g(t)=
| a |
| a |
| b |
| b |
可得△=4(
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
由二次函数的性质可知g(t)>0恒成立
∴当t=-
2
| ||||
2
|
|
| ||
|
|
即g(-
|
| ||
|
|
| b |
| b |
| b |
故当θ唯一确定时,|
| b |
故选:B
点评:本题考查平面向量数量级的运算,涉及二次函数的最值,属中档题.

练习册系列答案
相关题目
在平面直角坐标系中,O为原点,A(-1,0),B(0,
),C(3,0),动点D满足|
|=1,则|
+
+
|的取值范围是( )
| 3 |
| CD |
| OA |
| OB |
| OD |
| A、[4,6] | ||||
B、[
| ||||
C、[2
| ||||
D、[
|
阅读如图的程序框图,运行相应的程序,输出S的值为( )


| A、15 | B、105 |
| C、245 | D、945 |
设等差数列{an}的公差为d,若数列{2 a1an}为递减数列,则( )
| A、d>0 |
| B、d<0 |
| C、a1d>0 |
| D、a1d<0 |
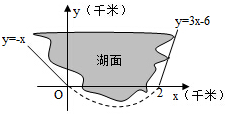 如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切),已知环湖弯曲路段为某三次函数图象的一部分,则该函数的解析式为( )
如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切),已知环湖弯曲路段为某三次函数图象的一部分,则该函数的解析式为( )A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
奇函数f(x)的定义域为R,若f(x+2)为偶函数,且f(1)=1,则f(8)+f(9)=( )
| A、-2 | B、-1 | C、0 | D、1 |
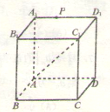 如图,P是正方体ABCD-A1B1C1D1棱A1D1上一点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的是
如图,P是正方体ABCD-A1B1C1D1棱A1D1上一点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的是